Regresión de cresta

La regresión de la cresta aborda algunos de los problemas de los mínimos cuadrados imponiendo una penalización sobre el tamaño de los coeficientes. Los coeficientes de cresta minimizan una suma residual penalizada de cuadrados,

Aquí, alpha >0 es un parámetro de complejidad que controla la cantidad de encogimiento: cuanto mayor es el valor de alfa, mayor es la cantidad de encogimiento y por lo tanto los coeficientes se vuelven más robustos a la colinearidad.

Al igual que con otros modelos lineales, la regresión de cresta tomará en su método de ajuste las matrices X, y y guardará los coeficientes w del modelo lineal en su miembro coef_.

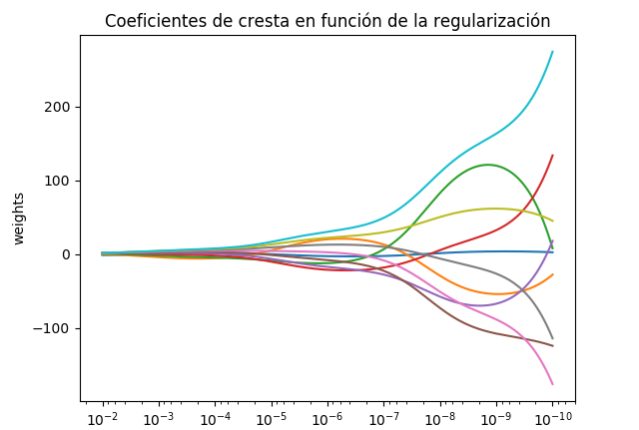
Coeficientes de Regresión de cresta en función de la regularización

Muestra el efecto de la colinealidad en los coeficientes de un estimador.

Regresión de cresta es el estimador utilizado en este ejemplo. Cada color representa una característica diferente del vector de coeficiente, y esto se muestra en función del parámetro de regularización.

Este ejemplo también muestra la utilidad de aplicar la regresión de cresta a matrices muy mal acondicionadas. Para estas matrices, un ligero cambio en la variable objetivo puede causar grandes variaciones en los pesos calculados. En tales casos, es útil establecer una cierta regularización (alfa) para reducir esta variación (ruido).

Cuando el alfa es muy grande, el efecto de regularización domina la función de pérdida cuadrada y los coeficientes tienden a cero. Al final del camino, como el alfa tiende hacia cero y la solución tiende hacia los mínimos cuadrados ordinarios, los coeficientes presentan grandes oscilaciones. En la práctica es necesario afinar el alfa de tal manera que se mantenga un equilibrio entre ambos.

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

# X es la 10x10 matrix de Hilbert
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)

n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)

coefs = []
for a in alphas:
ridge = linear_model.Ridge(alpha=a, fit_intercept=False)
ridge.fit(X, y)
coefs.append(ridge.coef_)

# mostramos resultados

ax = plt.gca()

ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
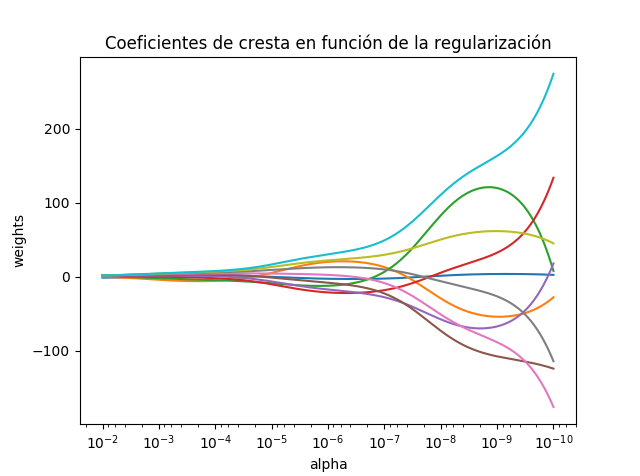
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Coeficientes de cresta en función de la regularización')
plt.axis('tight')
plt.show()

➡ Continúa aprendiendo de Machine Learning con nuestro curso:

Curso de Machine Learning en Python