Machine Learning Nearest Neighbour (vecinos mas cercanos)

sklearn.neighbors proporciona funcionalidad para métodos de aprendizaje basados en vecinos no supervisados y supervisados . Los vecinos más cercanos no supervisados son la base de muchos otros métodos de aprendizaje, especialmente el aprendizaje múltiple y la agrupación espectral. El aprendizaje supervisado basado en vecinos viene en dos formas: clasificación de datos con etiquetas discretas y regresión para datos con etiquetas continuas.

El principio detrás de los métodos vecinos más cercanos es encontrar un número predefinido de muestras de entrenamiento más cercanas al nuevo punto y predecir la etiqueta a partir de éstas. El número de muestras puede ser una constante definida por el usuario (aprendizaje del vecino más cercano) o variar según la densidad local de puntos (aprendizaje del vecino basado en el radio). La distancia puede, en general, ser cualquier medida métrica: la distancia estándar euclidiana es la opción más común. Los métodos basados en los vecinos son conocidos como métodos de aprendizaje automático no generalizantes, ya que simplemente “recuerdan” todos sus datos de entrenamiento).

A pesar de su simplicidad, los vecinos más cercanos han tenido éxito en un gran número de problemas de clasificación y regresión, incluyendo dígitos manuscritos o escenas de imágenes satelitales. Siendo un método no paramétrico, a menudo tiene éxito en situaciones de clasificación en las que la frontera de decisión es muy irregular.

Las clases en sklearn.neighbors pueden manejar matrices Numpy o Scipy.sparse matrices como entrada. Para matrices densas, se admite un gran número de métricas de distancia posibles. Para las matrices dispersas, las métricas arbitrarias de Minkowski son soportadas para búsquedas.

Nearest Neighbors Clasificacion

La clasificación basada en los vecinos es un tipo de aprendizaje basado en instancias o no generalizador: no intenta construir un modelo interno general, sino que simplemente almacena las instancias de los datos del entrenamiento. La clasificación se calcula a partir de un voto por mayoría simple de los vecinos más cercanos de cada punto: se asigna un punto de consulta a la clase de datos que tiene más representantes dentro de los vecinos más cercanos del punto.

scikit-learn implementa dos clasificadores diferentes de vecinos más cercanos: KNeighborsClassifier implementa el aprendizaje basado en los k vecinos más cercanos de cada punto de consulta, donde k es un valor entero especificado por el usuario. RadiusNeighborsClassifier implementa el aprendizaje en base al número de vecinos dentro de un radio fijo r de cada punto de entrenamiento, donde r es un valor de punto flotante especificado por el usuario.

La clasificación de k-neighbors en KNeighborsClassifier es la más comúnmente utilizada de las dos técnicas. La elección óptima del valor k depende en gran medida de los datos: en general, un valor k mayor suprime los efectos del ruido, pero hace que los límites de clasificación sean menos definidos.

En los casos donde los datos no son muestreados uniformemente, la clasificación de los vecinos basados en el radio en RadiusNeighborsClassifier puede ser una mejor opción. El usuario especifica un radio fijo r, de tal manera que los puntos en vecindarios más alejados utilizan menos vecinos cercanos para la clasificación. Para los espacios de parámetros de alta dimensión, este método se vuelve menos efectivo debido a la llamada “maldición de la dimensionalidad”.

La clasificación básica de los vecinos más cercanos utiliza pesos uniformes: es decir, el valor asignado a un punto de consulta se calcula a partir de una mayoría simple de votos de los vecinos más cercanos. Bajo algunas circunstancias, es mejor pesar a los vecinos de tal manera que los vecinos más cercanos contribuyan más al ajuste. Esto se puede lograr a través de pesas. El valor por defecto, weights =’ uniforme’, asigna pesos uniformes a cada vecino. weights =’ distancia’ asigna pesos proporcionales a la distancia inversa del punto de consulta. Alternativamente, se puede suministrar una función de la distancia definida por el usuario que se utiliza para calcular los pesos.

Ejemplo Nearest Neighbors Clasificacion

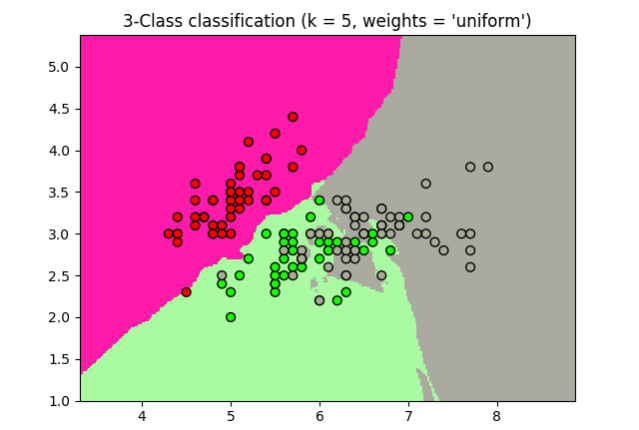
Uso de muestra de la clasificación de Vecinos más cercanos. Trazararemos los límites de decisión para cada clase:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets

n_neighbors = 15

# Importar algunos datos para jugar
iris = datasets.load_iris()

# en X solo tomamons coordenadas 2D
# y tiene los conjuntos de 0, 1 y 2
X = iris.data[:, :2]
y = iris.target

# tamaño del paso en la malla
h = .02

# Create color maps
cmap_light = ListedColormap(['#FF1AAA', '#AAFAA1', '#AAAAA1'])
cmap_bold = ListedColormap(['#FF0000', '#19FA05', '#AAAA99'])

for weights in ['uniform', 'distance']:
  # creamos una instancia de Clasificador de Vecinos y encajamos los datos.
  clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
  clf.fit(X, y)

  #Plotea el límite de decisión. Para ello, asignaremos un color a cada uno de ellos.
  # puntos de la malla [x_min, x_max]x[y_min, y_max].
  x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
  y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
  xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
  np.arange(y_min, y_max, h))
  Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

  # Pon el resultado con colores
  Z = Z.reshape(xx.shape)
  plt.figure()
  plt.pcolormesh(xx, yy, Z, cmap=cmap_light)

  # plotea tambien los puntos de entrenamiento
  plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,edgecolor='k', s=20)
  plt.xlim(xx.min(), xx.max())
  plt.ylim(yy.min(), yy.max())
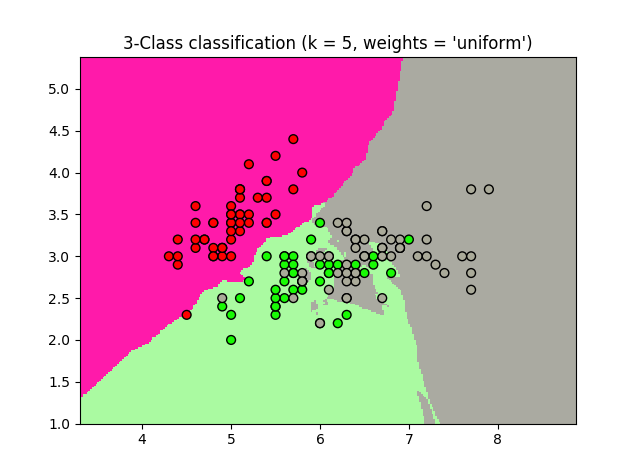
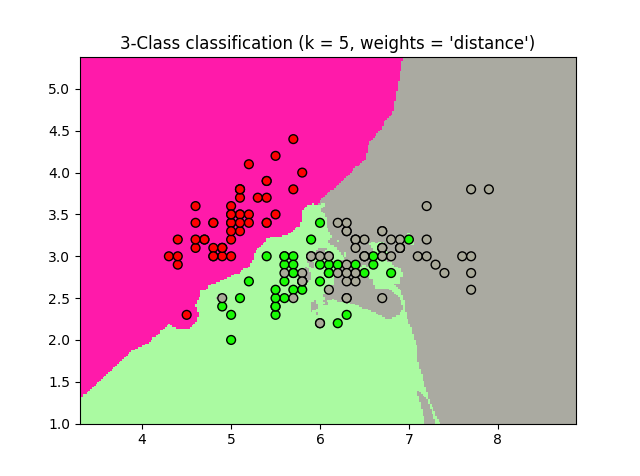
  plt.title("3-Class classification (k = %i, weights = '%s')"
            % (n_neighbors, weights))

plt.show()

Resultados del ejemplo Nearest Neighbors Clasificacion

➡ Continúa aprendiendo de Machine Learning con nuestro curso:

Curso de Machine Learning en Python