Descenso de Gradientes Estocástico “SGD”

El Descenso de Gradientes Estocástico (SGD) es un enfoque simple pero muy eficiente para el aprendizaje discriminatorio de clasificadores lineales bajo funciones de pérdida convexa tales como Máquinas Vectoriales de Soporte (lineal) y Regresión Logística. A pesar de que SGD ha estado presente en la comunidad de aprendizaje automático durante mucho tiempo, ha recibido una considerable cantidad de atención recientemente en el contexto del aprendizaje a gran escala.

SGD se ha aplicado con éxito a los problemas de aprendizaje a gran escala y escasa máquina de aprendizaje a menudo encontrados en la clasificación de textos y el procesamiento del lenguaje natural.

Las ventajas del descenso de gradiente estocástico son:

• Eficiencia.
• Facilidad de implementación (muchas oportunidades para el ajuste del código).

Las desventajas del descenso de gradiente estocástico incluyen:

• SGD requiere una serie de hiperparámetros como el parámetro de regularización y el número de iteraciones.
• SGD es sensible a la escala de las características.

Clasificacion del Descenso de Gradientes Estocástico

La clase SGDClassifier implementa una rutina de aprendizaje de descenso de gradiente estocástico simple que soporta diferentes funciones de pérdida y penalizaciones para la clasificación.
Al igual que otros clasificadores, el SGD debe estar equipado con dos matrices: una matriz X de tamaño[n_muestras, n_funciones] que contenga las muestras de formación, y una matriz Y de tamaño[n_muestras] que contenga los valores objetivo (etiquetas de clase) para las muestras de formación:

from sklearn.linear_model import SGDClassifier
X = [[0., 0.], [1., 1.]]
y = [0, 1]
clf = SGDClassifier(loss="hinge", penalty="l2")
clf.fit(X, y)

Después de la instalación, el modelo se puede utilizar para predecir nuevos valores:

clf.predict([[2., 2.]])

SGD ajusta un modelo lineal a los datos de entrenamiento. El miembro coef_ mantiene los parámetros del modelo:

clf.coef_

El miembro intercept_ mantiene la interceptación (también conocida como compensación o sesgo):

clf.intercept_

El parámetro fit_intercept controla si el modelo debe o no utilizar un interceptor, es decir, un hiperplano sesgado.

Para obtener la distancia firmada al hiperplano utilice SGDClassifier. decision_function:

clf.decision_function([[2., 2.]]) 

La función de pérdida concreta se puede ajustar a través del parámetro de loss. SGDClassifier soporta las siguientes funciones de pérdidas:

• loss=”hinge”: Máquina Vectorial de Soporte lineal (margen suave),
• loss=”modified_huber”: pérdida de bisagra suavizada,
• loss=”log”: regresión logística, y todas las pérdidas de regresión más abajo.

Las dos primeras funciones de pérdida son perezosas, sólo actualizan los parámetros del modelo si un ejemplo viola la restricción de margen, lo que hace que el entrenamiento sea muy eficiente y puede resultar en modelos de sparser, incluso cuando se usa la penalización L2.

El uso de loss=”log” o loss=”modified_huber” habilita el método predict_proba, que proporciona un vector de estimaciones de probabilidad P (y|x) por muestra x:

clf = SGDClassifier(loss="log").fit(X, y)
clf.predict_proba([[1., 1.]]) 

La penalización concreta se puede establecer a través del parámetro de penalty. SGD apoya las siguientes sanciones:

• penalty=”l2″: penalización de la norma L2 en coef_.
• penalty=”l1″: Pena de norma L1 en coef_.
• penalty=”elasticnet”: Combinación convexa de L2 y L1; (1 – relación l1) * L2 + relación l1 * L1.

El ajuste predeterminado es penalty=”l2″. La penalización L1 conduce a soluciones escasas, llevando la mayoría de los coeficientes a cero. La Red Elástica resuelve algunas deficiencias de la penalización L1 en presencia de atributos altamente correlacionados. El parámetro l1_ratio controla la combinación convexa de penalización L1 y L2.

SGDClassifier es compatible con la clasificación multiclase al combinar varios clasificadores binarios en un esquema de “uno contra todos” (OVA). Para cada una de las clases de K, se aprende un clasificador binario que discrimina entre esa y todas las demás clases de K-1. En el momento de la prueba, calculamos la puntuación de confianza (es decir, las distancias firmadas al hiperplano) para cada clasificador y elegimos la clase con la máxima confianza. La figura siguiente ilustra el enfoque OVA en el conjunto de datos del iris. Las líneas discontinuas representan los tres clasificadores OVA; los colores de fondo muestran la superficie de decisión inducida por los tres clasificadores.

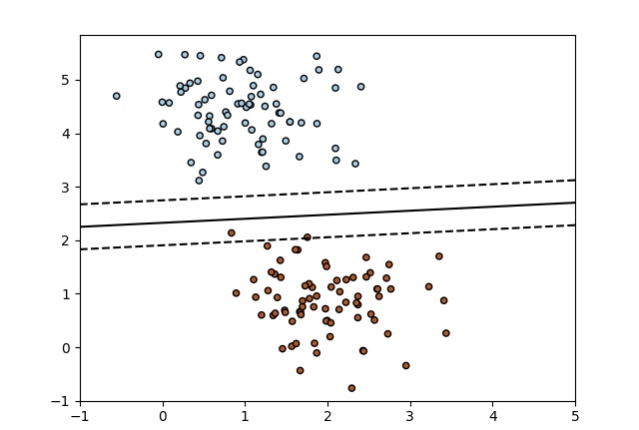
Ejemplo de SGD: Máximo margen de separación del hiperplano

Traza el margen máximo que separa el hiperplano dentro de un conjunto de datos separable de dos clases usando un clasificador lineal de máquinas vectoriales de soporte entrenado usando SGD.

Codigo python SGD: Máximo margen de separación del hiperplano

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDClassifier
from sklearn.datasets.samples_generator import make_blobs

# creamos 60 puntos separables
X, Y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60)

# ajusta el modelo
clf = SGDClassifier(loss="hinge", alpha=0.01, max_iter=200, fit_intercept=True)
clf.fit(X, Y)

# trazar la línea, los puntos y los vectores más cercanos al plano
xx = np.linspace(-1, 5, 10)
yy = np.linspace(-1, 5, 10)

X1, X2 = np.meshgrid(xx, yy)
Z = np.empty(X1.shape)
for (i, j), val in np.ndenumerate(X1):
  x1 = val
  x2 = X2[i, j]
  p = clf.decision_function([[x1, x2]])
  Z[i, j] = p[0]
levels = [-1.0, 0.0, 1.0]
linestyles = ['dashed', 'solid', 'dashed']
colors = 'k'
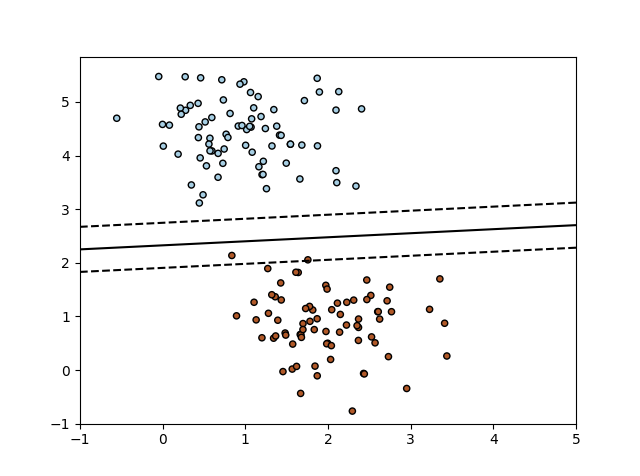
plt.contour(X1, X2, Z, levels, colors=colors, linestyles=linestyles)
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired,
edgecolor='black', s=20)

plt.axis('tight')
plt.show()

➡ Aprende mucho mas de Machine Learning con nuestro curso:

Curso de Machine Learning en Python