SVC lineal Machine Learning

El algoritmo de Machine Learning más aplicable para nuestros problemas más usuales es el SVC lineal. Antes de entrar en SVC lineal con nuestros datos, vamos a mostrar un ejemplo muy simple que le ayudará a solidificar su comprensión del SVC lineal.

El objetivo de un SVC lineal (Support Vector Classifier) es adecuarse a los datos que usted proporciona, devolviendo un hiperplano “ideal” que divide o categoriza sus datos. Desde allí, después de obtener el hiperplano, usted puede entonces alimentar algunas características a su clasificador para ver lo que es la clase “predecida”.

Primero, vamos a necesitar algunas dependencias básicas:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.svm import SVC

Matplotlib no es realmente necesario para el SVC lineal. La razón por la que lo estamos usando aquí es para la visualización de datos. Típicamente, usted no podrá visualizar tantas dimensiones como características tendrá, pero vale la pena visualizar al menos una vez para entender cómo funciona el SVC lineal.

Aparte de los paquetes de visualización que estamos usando, sólo necesitará importar svm desde sklearn y numpy para la conversión de array.

A continuación, consideremos que tenemos dos características a considerar. Estas características serán visualizadas como eje en nuestro gráfico. Así que algo parecido:

x = [2, 6, 1.5, 9, 3, 13]
y = [2, 9, 1.8, 8, 0.6, 11]

Entonces podemos graficar estos datos usando:

plt.scatter(x,y)
plt.show()

El resultado es:

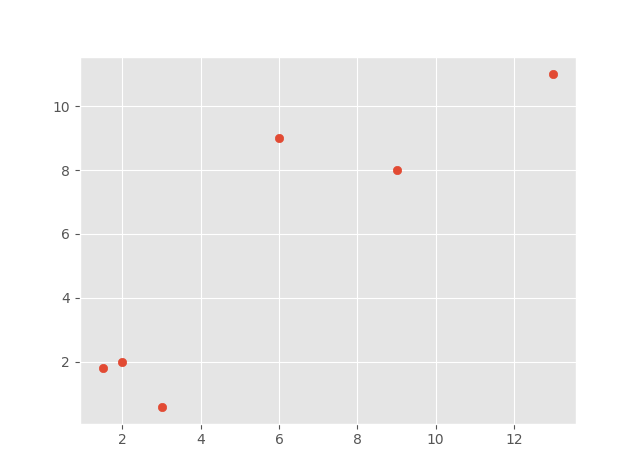
Ahora, por supuesto, podemos ver con nuestros propios ojos cómo se debe dividir a estos grupos, aunque es posible que se debata la línea divisoria:

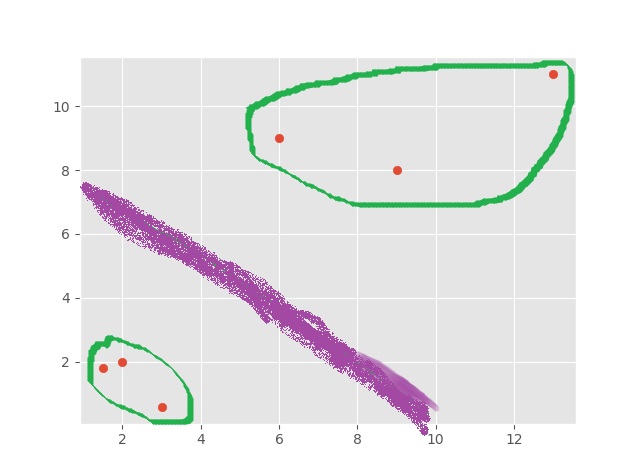
Así que vemos esto con dos características (2 grupos), y vemos que tenemos una gráfica 2D. Si tuviéramos tres características, podríamos tener un gráfico 3D. El gráfico en 3D sería un poco más desafiante para nosotros agrupar y dividir visualmente, pero aún así es posible hacerlo. El problema ocurre cuando tenemos cuatro características, o cuatro mil características. Ahora usted puede empezar a entender el poder del Machine Learning, viendo y analizando un número de dimensiones imperceptibles para nosotros.

Con esto en mente, vamos a seguir adelante y continuar con nuestro ejemplo de dos características. Ahora, para alimentar los datos a nuestro algoritmo de Machine Learning, primero necesitamos compilar una matriz de las características, en lugar de tenerlas como coordenadas x e y.

Generalmente, verá la lista de características guardada en una variable X mayúscula. Vamos a traducir nuestras coordenadas x e y en un array que es compilado de las coordenadas x e y, donde x es una característica y y es una característica.

X = np.array([[2,2],
 [6,9],
 [1.5,1.8],
 [9,8],
 [3,0.6],
 [13,11]])

Ahora que tenemos el vector , necesitamos etiquetarlo para propósitos de entrenamiento. Hay formas de Machine Learning llamadas “aprendizaje sin supervisión”, en las que no se utiliza el etiquetado de datos, como es el caso del clustering, aunque este ejemplo es una forma de aprendizaje supervisado.

Para nuestras etiquetas, a veces denominadas “objetivos”, vamos a usar 0 o 1.

y = [0,1,0,1,0,1]

Basta con mirar nuestro conjunto de datos para ver que tenemos pares de coordenadas que son números “bajos” y pares de coordenadas que son números “más altos”. Luego hemos asignado 0 a los pares de coordenadas inferiores y 1 a los pares de características superiores.

Estas son las etiquetas. En el caso de nuestro proyecto, terminaremos teniendo una lista de características numéricas que son estadísticas sobre las sociedades anónimas, y luego la “etiqueta” será un 0 o un 1, donde 0 es inferior al rendimiento del mercado y un 1 es superior al mercado.

Siguiendo adelante, ahora vamos a definir nuestro clasificador:

clf = SVC(kernel='linear', probability=True, tol=1e-3)

Vamos a utilizar el SVC (Support Vector Clasifier) SVM (Support Vector Machine). Nuestro kernel va a ser lineal.

Luego, llamamos:

clf.fit(X,y)

Nota: este es un tutorial más antiguo, y Scikit-Learn desde entonces ha desaprobado este método. En la versión 0.19, este código causará un error porque necesita ser un array numpy, y re-formado. Para ver un ejemplo de conversión a una matriz NumPy y remodelación, consulte este tutorial de K Nearest Neighbors, cerca del final. No es necesario que siga con esa serie para imitar lo que se hace allí con la remodelación, y continúe con esta serie.

Desde aquí, el aprendizaje está hecho. Correr el código debería de ser casi instantáneo, ya que tenemos un conjunto de datos tan pequeño.

Luego, podemos predecir y probar. Vamos a imprimir una predicción:

j=clf.predict([4.58,7.76])

Esperamos que esto prediga un 1, ya que es un par de coordenadas “alto”.

Ciertamente, la predicción es una clasificación de 1 porque j es igual a 1. Pero si hacemos j=clf.predict([0.58,0.7]) el resultado es j=0 por lo que todo funciona correctamente.

Estas fueron unas predicciones ciegas, aunque en realidad también fueron unas pruebas.

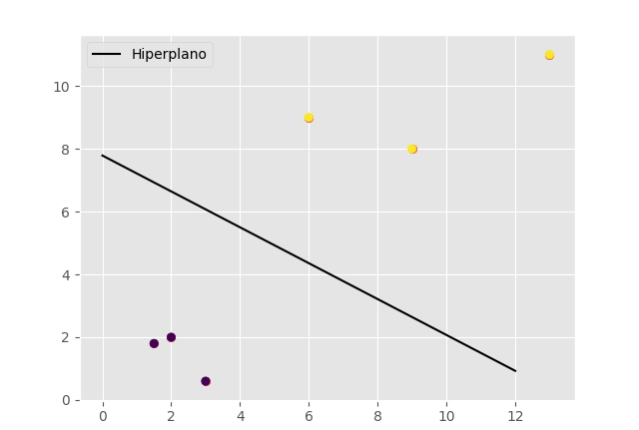
Visualizamos el hiperplano con los datos:

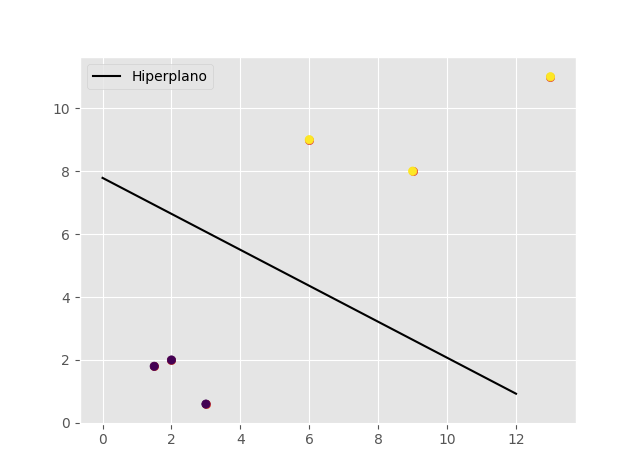
Código completo del ejemplo SVC lineal Machine Learning:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.svm import SVC

x = [2, 6, 1.5, 9, 3, 13]
y = [2, 9, 1.8, 8, 0.6, 11]

plt.scatter(x,y)
plt.show()


X = np.array([[2,2],
[6,9],
[1.5,1.8],
[9,8],
[3,0.6],
[13,11]])


y = [0,1,0,1,0,1]

clf = SVC(kernel='linear', probability=True, tol=1e-3)
clf.fit(X,y)

j=clf.predict([4.58,7.76])
j1=clf.predict([0.58,0.7])

w = clf.coef_[0]
print(w)

a = -w[0] / w[1]

xx = np.linspace(0,12)
yy = a * xx - clf.intercept_[0] / w[1]

h0 = plt.plot(xx, yy, 'k-', label="Hiperplano")

plt.scatter(X[:, 0], X[:, 1], c = y)
plt.legend()
plt.show()

➡ Aprende mucho mas de Machine Learning con nuestro curso:

Curso de Machine Learning en Python