Multiclass and multilabel algorithms / Algoritmos multiclase y multietiqueta

El módulo sklearn.multiclass implementa meta-estimuladores para resolver problemas de clasificación multiclase y multilabel descomponiendo dichos problemas en problemas de clasificación binaria. También se admite la regresión multiobjetivo.

• Clasificación multiclase significa una tarea de clasificación con más de dos clases; por ejemplo, clasificar un conjunto de imágenes de frutas que pueden ser naranjas, manzanas o peras. La clasificación multiclase parte del supuesto de que cada muestra está asignada a una sola etiqueta: una fruta puede ser una manzana o una pera, pero no ambas al mismo tiempo.
• La clasificación multilabel asigna a cada muestra un conjunto de etiquetas de destino. Esto puede pensarse como una predicción de las propiedades de un punto de datos que no son mutuamente excluyentes, como los temas que son relevantes para un documento. Un texto puede ser sobre cualquier religión, política, finanzas o educación al mismo tiempo o sobre ninguna de ellas.
• La regresión multisalida asigna a cada muestra un conjunto de valores objetivo. Se puede pensar que esto predice varias propiedades para cada punto de datos, como la dirección y magnitud del viento en un lugar determinado.
• La clasificación multiproducto-multiclase y la clasificación multitarea significa que un solo estimador tiene que realizar varias tareas conjuntas de clasificación. Esto es tanto una generalización de la tarea de clasificación multi-label, que sólo considera la clasificación binaria, como una generalización de la tarea de clasificación multi-clase. El formato de salida es un arreglo numérico 2d o matriz dispersa.

El conjunto de etiquetas puede ser diferente para cada variable de salida. Por ejemplo, a una muestra se le podría asignar “pera” para una variable de salida que toma valores posibles en un conjunto finito de especies como “pera”, “manzana”; y “azul” o “verde” para una segunda variable de salida que toma valores posibles en un conjunto finito de colores como “verde”, “rojo”, “azul”, “amarillo”…

Esto significa que cualquier clasificador que gestione tareas de clasificación multitarea o multiclase de salida, soporta la tarea de clasificación multietiqueta como un caso especial. La clasificación multitarea es similar a la tarea de clasificación multiproducto con diferentes formulaciones de modelos. Para más información, véase la documentación del estimador correspondiente.

Todos los clasificadores scikit-learn son capaces de clasificación multiclase, pero los meta-estimuladores ofrecidos por sklearn.multiclass permiten cambiar la forma en que manejan más de dos clases porque esto puede tener un efecto en el rendimiento del clasificador (ya sea en términos de error de generalización o recursos computacionales requeridos).

A continuación se muestra un resumen de los clasificadores soportados por scikit-learn agrupados por estrategia; no necesitas los meta-estimuladores de esta clase si estás usando uno de ellos, a menos que quieras un comportamiento multiclase personalizado:

• Inherentemente multiclase:
  sklearn.naive_bayes.BernoulliNB
  sklearn.tree.DecisionTreeClassifier
  sklearn.tree.ExtraTreeClassifier
  sklearn.ensemble.ExtraTreesClassifier
  sklearn.naive_bayes.GaussianNB
  sklearn.neighbors.KNeighborsClassifier
  sklearn.semi_supervisado.LabelPropagation
  sklearn.semi_supervisado.LabelSpreadading
  sklearn.discriminant_analysis.LinearDiscriminantAnalysis
  sklearn.svm.LinearSVC (configuración multi_class=”crammer_singer”)
  sklearn.linear_model.LogisticRegression (configuración multi_class=”multinomial”)
  sklearn.linear_model.LogisticRegressionCV (configuración multi_class=”multinomial”)
  sklearn.neural_network.MLPClassifier
  sklearn.neighbors.NearestCentroid
  sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis
  sklearn.neighbors.RadiusVecinosClasificador
  sklearn.ensemble.RandomForestClassifier
  sklearn.linear_model.RidgeClassifier
  sklearn.linear_model.RidgeClassifierCV
• Multiclase como One-Vs-One:
  sklearn.svm.NuSVC
  sklearn.svm.SVC.
  sklearn.gaussian_process.GaussianProcessClassifier (ajuste multi_clase = “one_vs_one”)
• Multiclase como One-Vs-Todos:
  sklearn.ensemble.GradientBoostingClassifier
  sklearn.gaussian_process.GaussianProcessClassifier (ajuste multi_clase = “one_vs_rest”)
  sklearn.svm.LinearSVC (configuración multi_class=”ovr”)
  sklearn.linear_model.LogisticRegression (configuración multi_class=”ovr”)
  sklearn.linear_model.LogisticRegressionCV (configuración multi_class=”ovr”)
  sklearn.linear_model.SGDClassifier
  sklearn.linear_model.Perceptron
  sklearn.linear_model.PassiveAggressiveClassifier
• Soporte multilabel:sklearn.tree.DecisionTreeClassifier
  sklearn.tree.ExtraTreeClassifier
  sklearn.ensemble.ExtraTreesClassifier
  sklearn.neighbors.KNeighborsClassifier
  sklearn.neural_network.MLPClassifier
  sklearn.neighbors.RadiusVecinosClasificador
  sklearn.ensemble.RandomForestClassifier
  sklearn.linear_model.RidgeClassifierCV
• Soporta multiclases-multiclases:sklearn.tree.DecisionTreeClassifier
  sklearn.tree.ExtraTreeClassifier
  sklearn.ensemble.ExtraTreesClassifier
  sklearn.neighbors.KNeighborsClassifier
  sklearn.neighbors.RadiusVecinosClasificador
  sklearn.ensemble.RandomForestClassifier

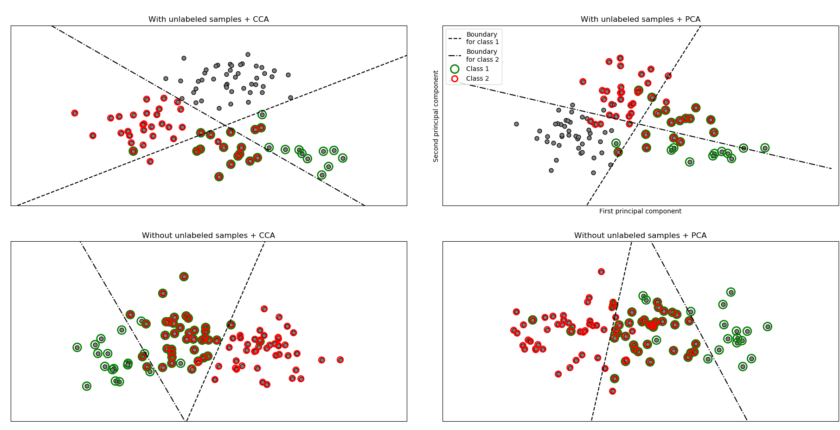
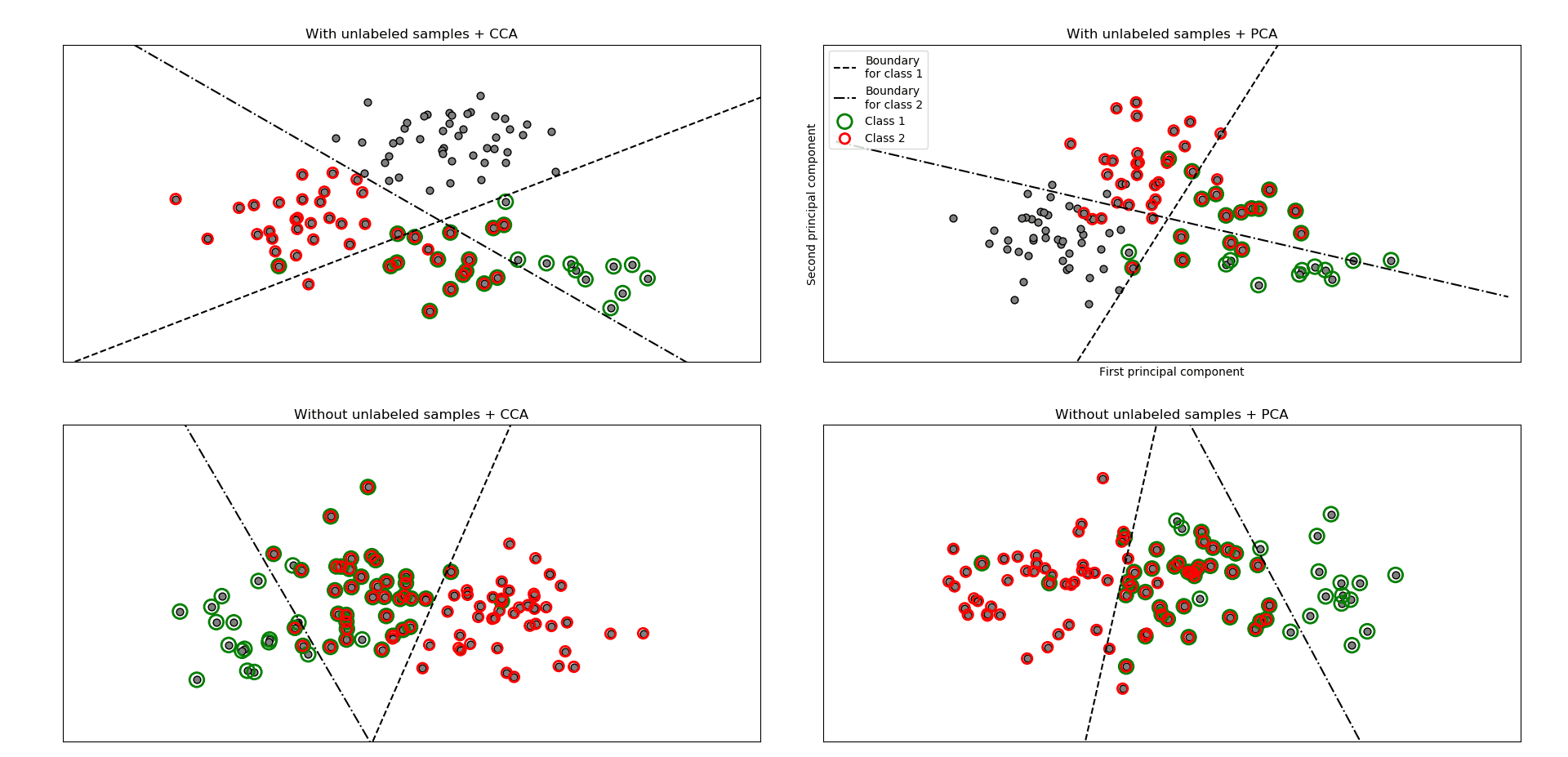
Ejemplo de Clasificación Multietiqueta

Este ejemplo simula un problema de clasificación de documentos de múltiples etiquetas. El dataset se genera aleatoriamente basado en el proceso siguiente:

• elegir el número de etiquetas: n ~ Poisson(n_labels)
• n veces, elija una clase c: c ~ Multinomial(theta)
• seleccionar la longitud del documento: k ~ Poisson(longitud)
• k veces, elija una palabra: w ~ Multinomial(theta_c)

El muestreo de rechazo se utiliza para asegurarse de que n es más de 2 y de que la longitud del documento nunca es cero. Asimismo, rechazamos las clases que ya han sido elegidas. Los documentos que se asignan a ambas clases se trazan rodeados de dos círculos coloreados.

La clasificación se realiza proyectando los dos primeros componentes principales encontrados por PCA y CCA para fines de visualización, seguido por el uso del metaclasificador sklearn.multiclass.OneVsRestClassifier utilizando dos SVCs con núcleos lineales para aprender un modelo discriminatorio para cada clase. Tenga en cuenta que PCA se utiliza para realizar una reducción de dimensionalidad no supervisada, mientras que CCA se utiliza para realizar una reducción de dimensionalidad supervisada.

Nota: en el gráfico, “muestras no etiquetadas” no significa que no conozcamos las etiquetas (como en el aprendizaje semi-supervisado) sino que las muestras simplemente no tienen una etiqueta.

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import make_multilabel_classification
from sklearn.multiclass import OneVsRestClassifier
from sklearn.svm import SVC
from sklearn.preprocessing import LabelBinarizer
from sklearn.decomposition import PCA
from sklearn.cross_decomposition import CCA

def plot_hyperplane(clf, min_x, max_x, linestyle, label):
  # separacion del hiperplano
  w = clf.coef_[0]
  a = -w[0] / w[1]
  xx = np.linspace(min_x - 5, max_x + 5) #estáte seguro que la línea es suficientemente larga
  yy = a * xx - (clf.intercept_[0]) / w[1]
  plt.plot(xx, yy, linestyle, label=label)

def plot_subfigure(X, Y, subplot, title, transform):
  if transform == "pca":
    X = PCA(n_components=2).fit_transform(X)
  elif transform == "cca":
    X = CCA(n_components=2).fit(X, Y).transform(X)
  else:
    raise ValueError

  min_x = np.min(X[:, 0])
  max_x = np.max(X[:, 0])

  min_y = np.min(X[:, 1])
  max_y = np.max(X[:, 1])

  classif = OneVsRestClassifier(SVC(kernel='linear'))
  classif.fit(X, Y)

  plt.subplot(2, 2, subplot)
  plt.title(title)

  zero_class = np.where(Y[:, 0])
  one_class = np.where(Y[:, 1])
  plt.scatter(X[:, 0], X[:, 1], s=40, c='gray', edgecolors=(0, 0, 0))
  plt.scatter(X[zero_class, 0], X[zero_class, 1], s=160, edgecolors='g', facecolors='none', linewidths=2, label='Class 1')
  plt.scatter(X[one_class, 0], X[one_class, 1], s=80, edgecolors='red', facecolors='none', linewidths=2, label='Class 2')

  plot_hyperplane(classif.estimators_[0], min_x, max_x, 'k--', 'Boundary\nfor class 1')
  plot_hyperplane(classif.estimators_[1], min_x, max_x, 'k-.', 'Boundary\nfor class 2')
  plt.xticks(())
  plt.yticks(())

  plt.xlim(min_x - .5 * max_x, max_x + .5 * max_x)
  plt.ylim(min_y - .5 * max_y, max_y + .5 * max_y)
  if subplot == 2:
    plt.xlabel('First principal component')
    plt.ylabel('Second principal component')
    plt.legend(loc="upper left")

plt.figure(figsize=(8, 6))

X, Y = make_multilabel_classification(n_classes=2, n_labels=1, allow_unlabeled=True, random_state=1)

plot_subfigure(X, Y, 1, "With unlabeled samples + CCA", "cca")
plot_subfigure(X, Y, 2, "With unlabeled samples + PCA", "pca")

X, Y = make_multilabel_classification(n_classes=2, n_labels=1, allow_unlabeled=False, random_state=1)

plot_subfigure(X, Y, 3, "Without unlabeled samples + CCA", "cca")
plot_subfigure(X, Y, 4, "Without unlabeled samples + PCA", "pca")

plt.subplots_adjust(.04, .02, .97, .94, .09, .2)
plt.show()

➡ Aprende mucho mas de Machine Learning con nuestro curso:

Curso de Machine Learning en Python