Ensemble methods o Métodos de conjunto

El objetivo de los métodos de conjunto es combinar las predicciones de varios estimadores de base construidos con un algoritmo de aprendizaje dado para mejorar la generalizabilidad/robustez sobre un solo estimador.

Por lo general, se distinguen dos familias de métodos de ensamblaje:

• En los métodos de promediación, el principio rector es construir varios estimadores independientemente y luego promediar sus predicciones. En promedio, el estimador combinado es usualmente mejor que cualquiera de los estimadores base porque su varianza es reducida.
• Por el contrario, en los métodos de empuje, los estimadores de base se construyen secuencialmente y se trata de reducir el sesgo del estimador combinado. La motivación es combinar varios modelos débiles para producir un conjunto poderoso.

Bagging meta-estimator o Meta-estimulador de ensacado

En los algoritmos de conjunto, los métodos de empaquetamiento forman una clase de algoritmos que construyen varias instancias de un estimador de caja negra en subconjuntos aleatorios del conjunto de entrenamiento original y luego agregan sus predicciones individuales para formar una predicción final. Estos métodos se utilizan como una forma de reducir la varianza de un estimador base (por ejemplo, un árbol de decisión), introduciendo la aleatorización en su procedimiento de construcción y luego formando un conjunto a partir de ella. En muchos casos, los métodos de ensacado constituyen una forma muy sencilla de mejorar respecto a un único modelo, sin necesidad de adaptar el algoritmo de base subyacente. Dado que proporcionan una manera de reducir el ajuste excesivo, los métodos de ensacado funcionan mejor con modelos fuertes y complejos (por ejemplo, árboles de decisión completamente desarrollados), en contraste con los métodos de refuerzo que generalmente funcionan mejor con modelos débiles (por ejemplo, árboles de decisión poco profundos).

Los métodos de Bagging vienen en muchos tipos, pero la mayoría difieren entre sí por la forma en que dibujan subconjuntos aleatorios del conjunto de entrenamiento:

• Cuando se dibujan subconjuntos aleatorios del conjunto de datos como subconjuntos aleatorios de las muestras, este algoritmo se conoce como Pasting.
• Cuando las muestras se toman con reemplazo, entonces el método se conoce como Bagging.
• Cuando los subconjuntos aleatorios del conjunto de datos se dibujan como subconjuntos aleatorios de las características, el método se conoce como Subespacios aleatorios.
• Por último, cuando los estimadores de base se construyen sobre subconjuntos de muestras y características, el método se conoce como Parches aleatorios.

En scikit-learn, los métodos de bagging se ofrecen como un meta-estimador unificado de BaggingClassifier (resp. BaggingRegressor), tomando como entrada un estimador de base especificado por el usuario junto con parámetros que especifican la estrategia para dibujar subconjuntos aleatorios. En particular, max_samples y max_features controlan el tamaño de los subconjuntos (en términos de muestras y características), mientras que bootstrap y bootstrap_features controlan si las muestras y características se dibujan con o sin reemplazo. Cuando se utiliza un subconjunto de las muestras disponibles, la precisión de generalización se puede estimar con las muestras fuera de bolsa configurando oob_score=True. Como ejemplo, el siguiente fragmento ilustra cómo instanciar un conjunto de estimadores de base de KNeighborsClassifier, cada uno construido sobre subconjuntos aleatorios del 50% de las muestras y el 50% de las características.

Ejemplo de Bagging meta-estimator

Estimador único versus ensacado: descomposición de varianza de sesgo

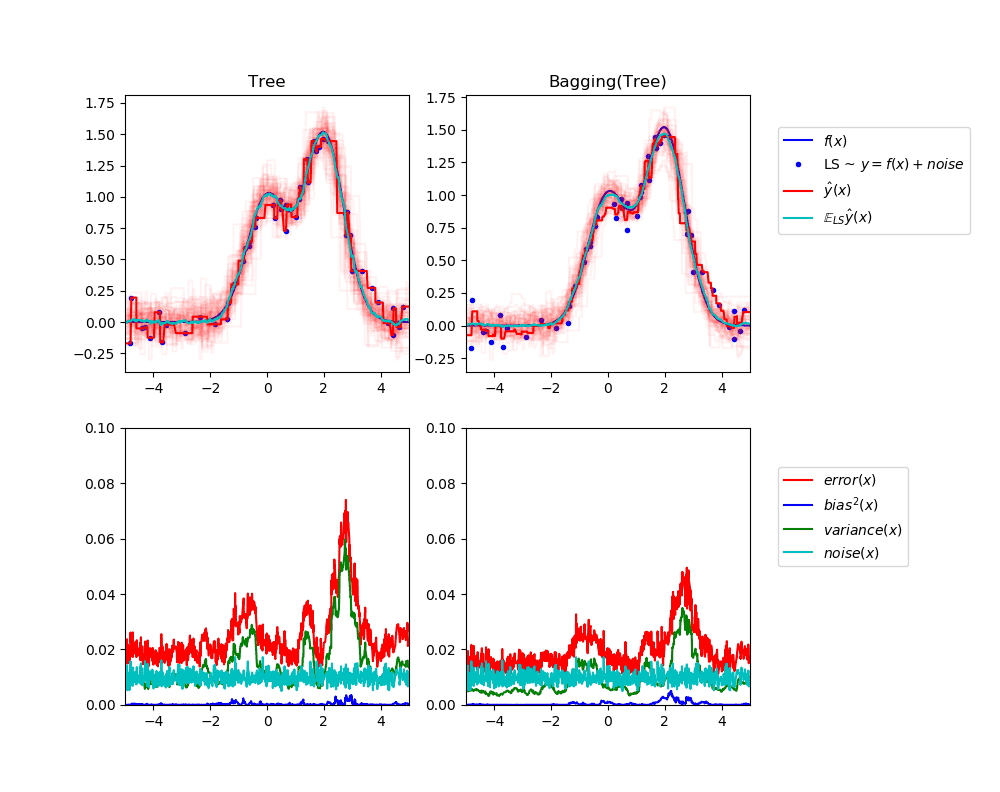
Este ejemplo ilustra y compara la descomposición de la varianza de sesgo de la media cuadrada de error esperado de un solo estimador contra un conjunto de ensamble de bagging.

En la regresión, el error cuadrado medio esperado de un estimador puede descomponerse en términos de sesgo, varianza y ruido. En promedio sobre los conjuntos de datos del problema de regresión, el término de sesgo mide la cantidad promedio por la cual las predicciones del estimador difieren de las predicciones del mejor estimador posible para el problema (es decir, el modelo Bayes). El término de varianza mide la variabilidad de las predicciones del estimador cuando se ajustan a diferentes instancias LS del problema. Finalmente, el ruido mide la parte irreductible del error que se debe a la variabilidad de los datos.

La figura superior izquierda ilustra las predicciones (en rojo oscuro) de un único árbol de decisión entrenado sobre un conjunto de datos aleatorio LS (los puntos azules) de un problema de regresión 1d de juguete. También ilustra las predicciones (en rojo claro) de otros árboles de decisión individuales entrenados sobre otros (y diferentes) ejemplos aleatorios LS del problema. Intuitivamente, el término de varianza aquí corresponde al ancho del haz de predicciones (en rojo claro) de los estimadores individuales. Cuanto mayor es la varianza, más sensibles son las predicciones de x a pequeños cambios en el conjunto de entrenamiento. El término de sesgo corresponde a la diferencia entre la predicción promedio del estimador (en cian) y el mejor modelo posible (en azul oscuro). Sobre este problema, podemos observar que el sesgo es bastante bajo (tanto la curva cian como la azul están cerca una de la otra) mientras que la varianza es grande (el haz rojo es bastante amplio).

La figura inferior izquierda muestra la descomposición por puntos del error promedio cuadrado esperado de un único árbol de decisión. Confirma que el término de sesgo (en azul) es bajo mientras que la varianza es grande (en verde). También ilustra la parte de ruido del error que, como se esperaba, parece ser constante y alrededor de 0,01.

Las cifras correctas corresponden a las mismas parcelas pero utilizando en su lugar un conjunto de árboles de decisión. En ambas figuras se observa que el término sesgo es mayor que en el caso anterior. En la figura superior derecha, la diferencia entre la predicción promedio (en cian) y el mejor modelo posible es mayor (por ejemplo, note el desplazamiento alrededor de x=2). En la figura inferior derecha, la curva de sesgo es también ligeramente más alta que en la figura inferior izquierda. Sin embargo, en términos de varianza, el haz de predicciones es más estrecho, lo que sugiere que la varianza es menor. De hecho, como confirma la cifra inferior derecha, el término de desviación (en verde) es inferior al de los árboles de decisión individuales. En general, la descomposición de la varianza de sesgo ya no es la misma. La compensación es mejor para el empaquetamiento: promediar varios árboles de decisión que encajan en las copias de arranque del conjunto de datos aumenta ligeramente el término de sesgo, pero permite una mayor reducción de la varianza, lo que resulta en un menor error de cuadrado medio general (compare las curvas rojas en las cifras inferiores). La salida del guión también confirma esta intuición. El error total del conjunto de ensacado es menor que el error total de un único árbol de decisión, y esta diferencia se debe principalmente a una varianza reducida.

import numpy as np
import matplotlib.pyplot as plt

from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor

# ajustes
n_repeat = 50 # numero de iteraciones
n_train = 50 # tamaño del set de entrenamiento
n_test = 1000 # tamaño del set de test
noise = 0.1 # desviacion estander de ruido
np.random.seed(0)

# Cambia esto por explorar la descomposición sesgo-varianza de otros 
# estimadores. Esto debería funcionar bien para estimadores con alta varianza (por ejemplo, 
# árboles de decisión o KNN), pero mal para estimadores con baja varianza (por ejemplo, 
# modelos lineales).
estimators = [("Tree", DecisionTreeRegressor()), ("Bagging(Tree)", BaggingRegressor(DecisionTreeRegressor()))]

n_estimators = len(estimators)

# generacion de datos
def f(x):
  x = x.ravel()

  return np.exp(-x ** 2) + 1.5 * np.exp(-(x - 2) ** 2)

def generate(n_samples, noise, n_repeat=1):
  X = np.random.rand(n_samples) * 10 - 5
  X = np.sort(X)

  if n_repeat == 1:
    y = f(X) + np.random.normal(0.0, noise, n_samples)
  else:
    y = np.zeros((n_samples, n_repeat))

    for i in range(n_repeat):
      y[:, i] = f(X) + np.random.normal(0.0, noise, n_samples)

  X = X.reshape((n_samples, 1))

  return X, y

X_train = []
y_train = []

for i in range(n_repeat):
  X, y = generate(n_samples=n_train, noise=noise)
  X_train.append(X)
  y_train.append(y)

X_test, y_test = generate(n_samples=n_test, noise=noise, n_repeat=n_repeat)

plt.figure(figsize=(10, 8))

# Estimadores de bucle para comparar
for n, (name, estimator) in enumerate(estimators):
  # computacion de predicciones
  y_predict = np.zeros((n_test, n_repeat))

  for i in range(n_repeat):
    estimator.fit(X_train[i], y_train[i])
    y_predict[:, i] = estimator.predict(X_test)
  #sesgo^2 + Variación + Descomposición del ruido del error promedio al cuadrado
  y_error = np.zeros(n_test)

  for i in range(n_repeat):
    for j in range(n_repeat):
      y_error += (y_test[:, j] - y_predict[:, i]) ** 2

  y_error /= (n_repeat * n_repeat)

  y_noise = np.var(y_test, axis=1)
  y_bias = (f(X_test) - np.mean(y_predict, axis=1)) ** 2
  y_var = np.var(y_predict, axis=1)

  print("{0}: {1:.4f} (error) = {2:.4f} (bias^2) "" + {3:.4f} (var) + {4:.4f} (noise)".format(name, np.mean(y_error), np.mean(y_bias), np.mean(y_var), np.mean(y_noise)))

  # representamos figuras
  plt.subplot(2, n_estimators, n + 1)
  plt.plot(X_test, f(X_test), "b", label="$f(x)$")
  plt.plot(X_train[0], y_train[0], ".b", label="LS ~ $y = f(x)+noise$")

  for i in range(n_repeat):
    if i == 0:
      plt.plot(X_test, y_predict[:, i], "r", label="$\^y(x)$")
    else:
      plt.plot(X_test, y_predict[:, i], "r", alpha=0.05)

  plt.plot(X_test, np.mean(y_predict, axis=1), "c", label="$\mathbb{E}_{LS} \^y(x)$")

  plt.xlim([-5, 5])
  plt.title(name)

  if n == n_estimators - 1:
    plt.legend(loc=(1.1, .5))

  plt.subplot(2, n_estimators, n_estimators + n + 1)
  plt.plot(X_test, y_error, "r", label="$error(x)$")
  plt.plot(X_test, y_bias, "b", label="$bias^2(x)$"),
  plt.plot(X_test, y_var, "g", label="$variance(x)$"),
  plt.plot(X_test, y_noise, "c", label="$noise(x)$")

  plt.xlim([-5, 5])
  plt.ylim([0, 0.1])

  if n == n_estimators - 1:

    plt.legend(loc=(1.1, .5))

plt.subplots_adjust(right=.75)
plt.show()

➡ ¿Quieres aprender mas de Machine Learning? Ingresa a nuestro curso:

Curso de Machine Learning en Python