Descomposición cruzada

El módulo de descomposición cruzada contiene dos familias principales de algoritmos: los mínimos cuadrados parciales (PLS) y el análisis de correlación canónica (CCA).

Estas familias de algoritmos son útiles para encontrar relaciones lineales entre dos conjuntos de datos multivariados: los argumentos X e Y del método fit son matrices 2D.

Los algoritmos de descomposición cruzada encuentran las relaciones fundamentales entre dos matrices (X e Y). Son enfoques variables latentes para modelar las estructuras de covarianza en estos dos espacios. Tratarán de encontrar la dirección multidimensional en el espacio X que explique la dirección de varianza multidimensional máxima en el espacio Y. La regresión PLS es particularmente adecuada cuando la matriz de predictores tiene más variables que observaciones, y cuando hay multicolinealidad entre los valores de X. Por el contrario, la regresión estándar fracasará en estos casos.

Ejemplo de Descomposición cruzada

Utilización sencilla de diversos algoritmos de descomposición cruzada:

– PLSCanónicos

– PLSRegresión, con respuesta multivariante, también denominada PLS2

– PLSRegresión, con respuesta univariante, también denominada PLS1

– CCA

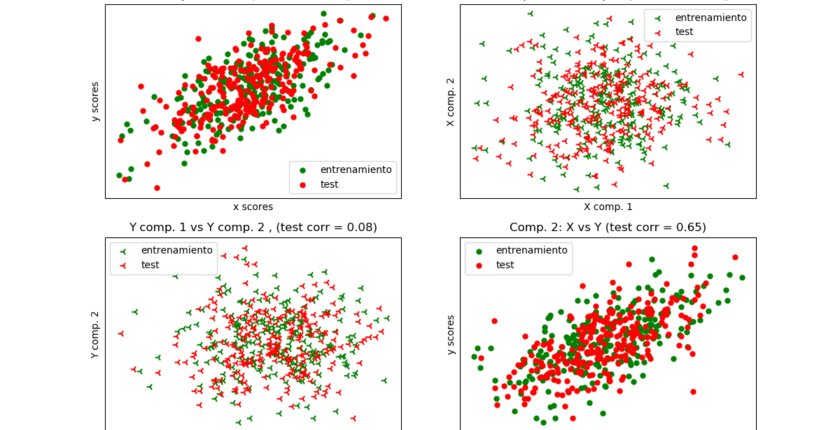
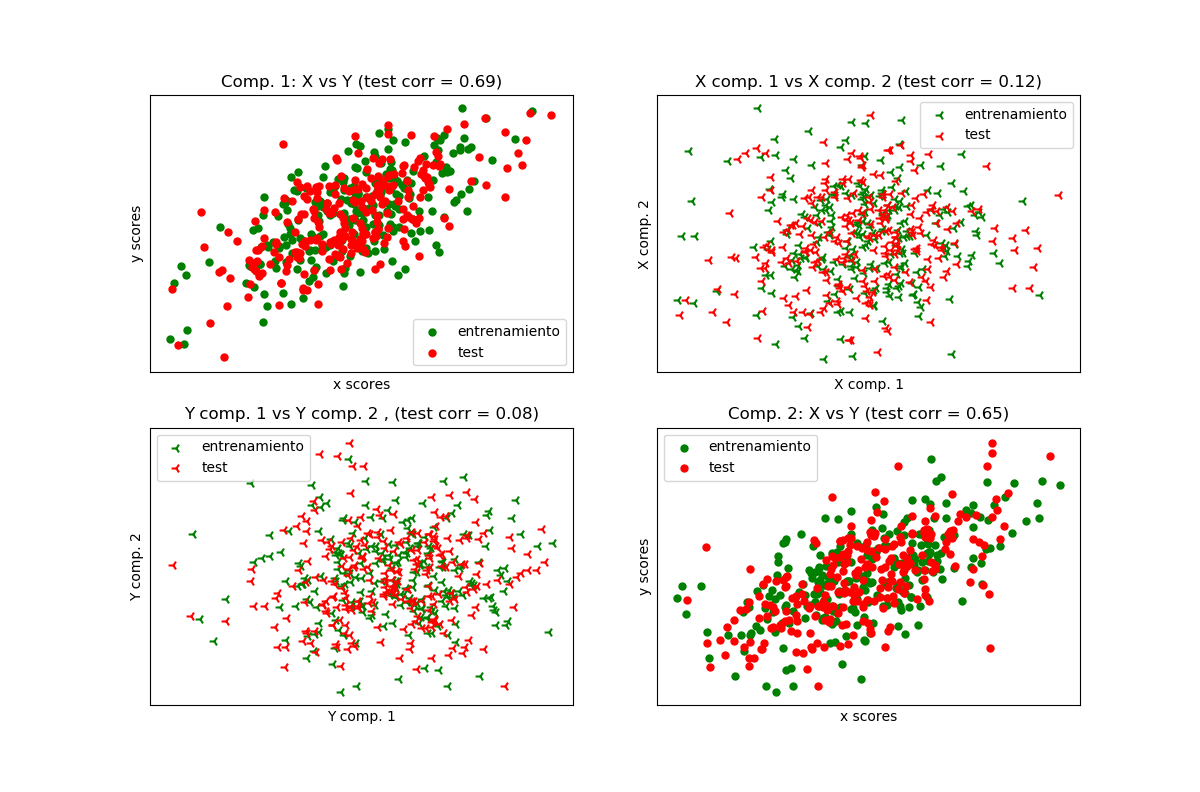
Dados 2 conjuntos de datos bidimensionales de covarianza multivariante, X, e Y, PLS extrae las “direcciones de covarianza”, es decir, los componentes de cada uno de los conjuntos de datos que explican la varianza más compartida entre ambos conjuntos de datos. Esto es evidente en la visualización de la matriz de diagrama de dispersión: los componentes 1 en el conjunto de datos X y el conjunto de datos Y están correlacionados al máximo (los puntos se encuentran alrededor de la primera diagonal). Esto también es cierto para los componentes 2 en ambos conjuntos de datos, sin embargo, la correlación entre los conjuntos de datos para los diferentes componentes es débil: la nube de puntos es muy esférica.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSCanonical, PLSRegression, CCA

# #############################################################################
# Modelo de variables latentes basado en conjuntos de datos

n = 500
# 2 vars latentes:
l1 = np.random.normal(size=n)
l2 = np.random.normal(size=n)

latents = np.array([l1, l1, l2, l2]).T
X = latents + np.random.normal(size=4 * n).reshape((n, 4))
Y = latents + np.random.normal(size=4 * n).reshape((n, 4))

X_train = X[:n // 2]
Y_train = Y[:n // 2]
X_test = X[n // 2:]
Y_test = Y[n // 2:]

print("Corr(X)")
print(np.round(np.corrcoef(X.T), 2))
print("Corr(Y)")
print(np.round(np.corrcoef(Y.T), 2))

# #############################################################################
# Canonical (simetria) PLS

# Transformacion de datos
# ~~~~~~~~~~~~~~
plsca = PLSCanonical(n_components=2)
plsca.fit(X_train, Y_train)
X_train_r, Y_train_r = plsca.transform(X_train, Y_train)
X_test_r, Y_test_r = plsca.transform(X_test, Y_test)

# ~~~~~~~~~~~~~~~~~~~~~~
# 1) En el diagrama diagonal, las puntuaciones X vs Y de cada componente
plt.figure(figsize=(12, 8))
plt.subplot(221)
plt.scatter(X_train_r[:, 0], Y_train_r[:, 0], label="entrenamiento",
marker="o", c="g", s=25)
plt.scatter(X_test_r[:, 0], Y_test_r[:, 0], label="test",
marker="o", c="r", s=25)
plt.xlabel("x scores")
plt.ylabel("y scores")
plt.title('Comp. 1: X vs Y (test corr = %.2f)' %
np.corrcoef(X_test_r[:, 0], Y_test_r[:, 0])[0, 1])
plt.xticks(())
plt.yticks(())
plt.legend(loc="best")

plt.subplot(224)
plt.scatter(X_train_r[:, 1], Y_train_r[:, 1], label="entrenamiento",
marker="o", c="g", s=25)
plt.scatter(X_test_r[:, 1], Y_test_r[:, 1], label="test",
marker="o", c="r", s=25)
plt.xlabel("x scores")
plt.ylabel("y scores")
plt.title('Comp. 2: X vs Y (test corr = %.2f)' %
np.corrcoef(X_test_r[:, 1], Y_test_r[:, 1])[0, 1])
plt.xticks(())
plt.yticks(())
plt.legend(loc="best")

# 2) Componentes de diagonal 1 vs 2 para X e Y
plt.subplot(222)
plt.scatter(X_train_r[:, 0], X_train_r[:, 1], label="entrenamiento",
marker="3", c="g", s=50)
plt.scatter(X_test_r[:, 0], X_test_r[:, 1], label="test",
marker="3", c="r", s=50)
plt.xlabel("X comp. 1")
plt.ylabel("X comp. 2")
plt.title('X comp. 1 vs X comp. 2 (test corr = %.2f)'
% np.corrcoef(X_test_r[:, 0], X_test_r[:, 1])[0, 1])
plt.legend(loc="best")
plt.xticks(())
plt.yticks(())

plt.subplot(223)
plt.scatter(Y_train_r[:, 0], Y_train_r[:, 1], label="entrenamiento",
marker="3", c="g", s=50)
plt.scatter(Y_test_r[:, 0], Y_test_r[:, 1], label="test",
marker="3", c="r", s=50)
plt.xlabel("Y comp. 1")
plt.ylabel("Y comp. 2")
plt.title('Y comp. 1 vs Y comp. 2 , (test corr = %.2f)'
% np.corrcoef(Y_test_r[:, 0], Y_test_r[:, 1])[0, 1])
plt.legend(loc="best")
plt.xticks(())
plt.yticks(())
plt.show()

# #############################################################################
# Regresión PLS, con respuesta multivariante, también denominada PLS2

n = 1000
q = 3
p = 10
X = np.random.normal(size=n * p).reshape((n, p))
B = np.array([[1, 2] + [0] * (p - 2)] * q).T
# cada Yj = 1*X1 + 2*X2 + ruido
Y = np.dot(X, B) + np.random.normal(size=n * q).reshape((n, q)) + 5

pls2 = PLSRegression(n_components=3)
pls2.fit(X, Y)
print("Verdadero B (como: Y = XB + Err)")
print(B)
# compare pls2.coef_ with B
print("Estimado B")
print(np.round(pls2.coef_, 1))
pls2.predict(X)

# Regresión PLS, con respuesta univariada, también denominada PLS1

n = 1000
p = 10
X = np.random.normal(size=n * p).reshape((n, p))
y = X[:, 0] + 2 * X[:, 1] + np.random.normal(size=n * 1) + 5
pls1 = PLSRegression(n_components=3)
pls1.fit(X, y)
#note que el número de componentes excede 1 (la dimensión de y)
print("Estimado betas")
print(np.round(pls1.coef_, 1))

# #############################################################################
#CCA (modo B PLS con deflación simétrica)

cca = CCA(n_components=2)
cca.fit(X_train, Y_train)
X_train_r, Y_train_r = cca.transform(X_train, Y_train)
X_test_r, Y_test_r = cca.transform(X_test, Y_test)

Salida por consola:

Corr(X)
[[ 1. 0.51 0.05 0.06]
 [ 0.51 1. 0.03 0.04]
 [ 0.05 0.03 1. 0.46]
 [ 0.06 0.04 0.46 1. ]]
Corr(Y)
[[ 1. 0.46 0.08 0.02]
 [ 0.46 1. 0.02 -0.01]
 [ 0.08 0.02 1. 0.47]
 [ 0.02 -0.01 0.47 1. ]]
Verdadero B (como: Y = XB + Err)
[[1 1 1]
 [2 2 2]
 [0 0 0]
 ..., 
 [0 0 0]
 [0 0 0]
 [0 0 0]]
Estimado B
[[ 0.9 1. 1. ]
 [ 2. 2. 2. ]
 [ 0. -0. -0. ]
 ..., 
 [ 0. 0. 0. ]
 [-0. -0. 0. ]
 [-0. -0. -0. ]]
Estimado betas
[[ 1.]
 [ 2.]
 [ 0.]
 [ 0.]
 [-0.]
 [-0.]
 [ 0.]
 [-0.]
 [-0.]
 [-0.]]

➡ Aprende mucho mas de Machine Learning con nuestro curso:

Curso de Machine Learning en Python

as for cons, babwigs.org are more expensive and need high maintenance.