Decision Trees o Árboles de decisión

Los Árboles de Decisión (DTs) son un método de aprendizaje supervisado no paramétrico utilizado para la clasificación y regresión. El objetivo es crear un modelo que prediga el valor de una variable objetivo mediante el aprendizaje de reglas de decisión simples inferidas a partir de las características de los datos.

Por ejemplo, en el ejemplo siguiente, los árboles de decisión aprenden de los datos para aproximar una curva sinusoidal con un conjunto de reglas de decisión if-then-else. Cuanto más profundo sea el árbol, más complejas serán las reglas de decisión y más adecuado será el modelo.

Algunas de las ventajas de los árboles de decisión son:

• Fácil de entender e interpretar. Los árboles pueden ser visualizados.
• Requiere poca preparación de datos. Otras técnicas requieren a menudo la normalización de los datos, la creación de variables ficticias y la eliminación de valores en blanco. Tenga en cuenta, sin embargo, que este módulo no admite los valores que faltan.
• El costo de usar el árbol (es decir, predecir datos) es logarítmico en el número de puntos de datos usados para entrenar al árbol.
• Capaz de manejar datos numéricos y categóricos. Otras técnicas suelen estar especializadas en el análisis de conjuntos de datos que sólo tienen un tipo de variable.
• Capaz de manejar problemas de múltiples salidas.
• Utiliza un modelo de caja blanca. Si una situación dada es observable en un modelo, la explicación de la condición se explica fácilmente por la lógica booleana. Por el contrario, en un modelo de caja negra (por ejemplo, en una red neural artificial), los resultados pueden ser más difíciles de interpretar.
• Posibilidad de validar un modelo mediante pruebas estadísticas. Esto permite dar cuenta de la fiabilidad del modelo.
  Funciona bien incluso si sus suposiciones son algo violadas por el verdadero modelo a partir del cual se generaron los datos.

Las desventajas de los árboles de decisión incluyen:

• Los alumnos del árbol de decisiones pueden crear árboles demasiado complejos que no generalizan bien los datos. A esto se le llama sobreequipamiento. Mecanismos tales como la poda (no soportada actualmente), la fijación del número mínimo de muestras requeridas en un nudo de la hoja o la fijación de la profundidad máxima del árbol son necesarios para evitar este problema.
• Los árboles de decisión pueden ser inestables porque pequeñas variaciones en los datos pueden resultar en la generación de un árbol completamente diferente. Este problema se mitiga utilizando árboles de decisión dentro de un conjunto.
• El problema de aprender un árbol de decisión óptimo es conocido por ser NP-completo bajo varios aspectos de optimización e incluso para conceptos simples. En consecuencia, los algoritmos prácticos de aprendizaje del árbol de decisión se basan en algoritmos heurísticos como el algoritmo codicioso, en el que se toman decisiones óptimas a nivel local en cada nodo. Tales algoritmos no pueden garantizar que devuelvan el árbol de decisión globalmente óptimo. Esto puede ser mitigado entrenando a múltiples árboles en un grupo de estudiantes, donde las características y muestras son muestreadas al azar con reemplazo.
• Hay conceptos que son difíciles de aprender porque los árboles de decisión no los expresan fácilmente, como XOR, paridad o problemas de multiplexor.
• Los participantes del árbol de decisión crean árboles sesgados si algunas clases dominan. Por lo tanto, se recomienda equilibrar el conjunto de datos antes de ajustarlo al árbol de decisión.

Ejemplo de Árboles de decisión

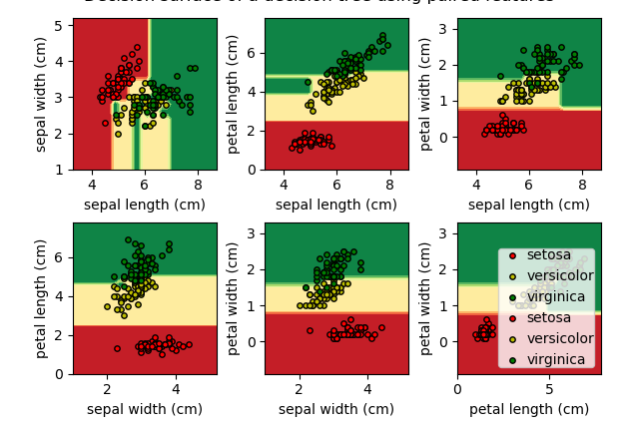
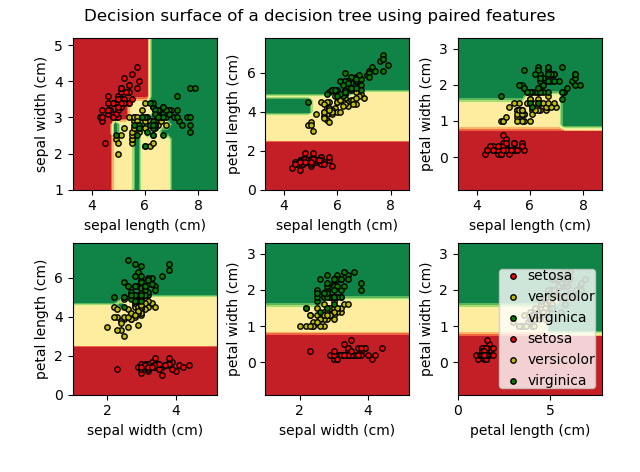
Trazar la superficie de decisión de un árbol de decisión en el conjunto de datos del iris

Trazar la superficie de decisión de un árbol de decisión entrenado en pares de características del conjunto de datos del iris.

Para cada par de características del iris, el árbol de decisión aprende límites de decisión hechos de combinaciones de reglas de umbral simples inferidas de las muestras de entrenamiento.

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

# Parametros
n_classes = 3
plot_colors = "ryg"
plot_step = 0.2

# Carga de datos
iris = load_iris()

for pairidx, pair in enumerate([[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]]):
  # Solo nos centramos en 2 caracteristicas
  X = iris.data[:, pair]
  y = iris.target

  # entrenamiento
  clf = DecisionTreeClassifier().fit(X, y)

  # ploteamos la desicion de frontera
  plt.subplot(2, 3, pairidx + 1)

  x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
  y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
  xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
  np.arange(y_min, y_max, plot_step))
  plt.tight_layout(h_pad=0.5, w_pad=0.5, pad=2.5)

  Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
  Z = Z.reshape(xx.shape)
  cs = plt.contourf(xx, yy, Z, cmap=plt.cm.RdYlGn)

  plt.xlabel(iris.feature_names[pair[0]])
  plt.ylabel(iris.feature_names[pair[1]])

  # ploteamos los puntos de entrenamiento
  for i, color in zip(range(n_classes), plot_colors):
    idx = np.where(y == i)
    plt.scatter(X[idx, 0], X[idx, 1], c=color, label=iris.target_names[i], cmap=plt.cm.RdYlBu, edgecolor='black', s=15)

plt.suptitle("Superficie de decisión de un árbol de decisión utilizando características apareadas")
plt.legend(loc='lower right', borderpad=0, handletextpad=0)
plt.axis("tight")
plt.show()

➡ ¿Quieres aprender mas de Machine Learning? Ingresa a nuestro curso:

Curso de Machine Learning en Python