Blog
Predicción de Series Temporales con Perceptrones Multicapa
- Publicado por: Rafael Fernandez
- Categoría: Deep Learning
-En esta lección descubrirá cómo desarrollar modelos de redes neuronales para la predicción de series temporales en Python usando la biblioteca de aprendizaje profundo de Keras.
-Predecir series de tiempo univariadas con el problema sobre los pasajeros de las aerolíneas.
-Cómo expresar la predicción de series temporales como un problema de regresión y desarrollar una red neuronal modelo para ello.
-Cómo enmarcar la predicción de series temporales con un desfase temporal y desarrollar un modelo de red neuronal por ello.
La predicción de series de tiempo es un problema difícil de resolver con el aprendizaje automático.
Descripción del problema: Predicción de series cronológicas
El problema que vamos a analizar en esta lección es el problema de la predicción de los pasajeros de las aerolíneas internacionales. Se trata de un problema en el que, al cabo de un año y un mes, la tarea consiste en predecir el número de pasajeros de líneas aéreas internacionales en unidades de 1.000. Los datos van de enero de 1949 a diciembre de 1960 o 12 años, con 144 observaciones. El conjunto de datos está disponible de forma gratuita en la página web de DataMarket como una descarga CSV con el nombre international-airline-passengers.csv o tambien lo puedes descargar desde aquí international-airline-passengers

Se puede ver una tendencia al alza en el gráfico. También se puede ver cierta periodicidad en el conjunto de datos que probablemente corresponde al período de vacaciones de verano del hemisferio norte.
Vamos a mantener las cosas simples y trabajar con los datos tal como están. Normalmente, es una buena idea investigar varias técnicas de preparación de datos para reescalar los datos y hacerlos estacionarios.
Regresión del Perceptrón Multicapa
Expresaremos el problema de predicción de series de tiempo como un problema de regresión. Es decir, dado el número de pasajeros (en unidades de miles) este mes, cuál es el número de pasajeros del próximo mes. Podemos escribir una función simple para convertir nuestra única columna de datos en un conjunto de datos de dos columnas. La primera columna que contiene el recuento de pasajeros de este mes (t) y la segunda columna que contiene el recuento de pasajeros del mes siguiente (t+1), que debe predecirse. Antes de empezar, primero importamos todas las funciones y clases que pretendemos usar.
import numpy import matplotlib.pyplot as plt from pandas import read_csv import math from keras.models import Sequential from keras.layers import Dense # semilla aleatoria para rerpoducibilidad numpy.random.seed(7)
También podemos usar el código de la sección anterior para cargar el conjunto de datos como un marco de datos de Pandas. Entonces podemos extraer la matriz NumPy del marco de datos y convertir los valores enteros en valores de coma flotante que son más adecuados para modelar con una red neuronal.
# cargamos el conjunto de datos
dataframe = read_csv('international-airline-passengers.csv', usecols=[1], engine='python', skipfooter=3)
dataset = dataframe.values
dataset = dataset.astype('float32')
Después de modelar nuestros datos y estimar la habilidad de nuestro modelo en el conjunto de datos de capacitación, nosotros necesitamos tener una idea de la habilidad del modelo en datos nuevos e invisibles. Para una clasificación normal o problema de regresión, lo haríamos utilizando la validación cruzada k-fold. Con datos de series temporales, la secuencia de valores es importante. Un método simple que podemos utilizar es dividir el orden en conjuntos de datos de entreno y de prueba. El siguiente código calcula el índice del punto de división y separa los datos en los conjuntos de datos de formación con el 67% de las observaciones que podemos utilizar para entrenar a nuestro modelo, dejando el 33% restante para probar el modelo.
#dividimos datos en entreno y datos para el test train_size = int(len(dataset) * 0.67) test_size = len(dataset) - train_size train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:] print(len(train), len(test))
Ahora podemos ejecutar una función para crear un nuevo conjunto de datos tal y como se ha descrito anteriormente. La función toma dos argumentos, el conjunto de datos que es un array NumPy que queremos convertir en un conjunto de datos y el look_back, que es el número de pasos de tiempo previos que se deben utilizar como variables de entrada para predecir el siguiente período de tiempo, en este caso, por defecto es 1. Este valor por defecto creará un conjunto de datos donde X es el número de pasajeros en un momento dado (t) e Y es el número de pasajeros en el momento siguiente de tiempo (t+1). Puede ser configurado y miraremos en la construcción de un conjunto de datos de forma diametralmente opuesta en la siguiente sección.
# convertir un array de valores en una matriz de conjuntos de datos
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return numpy.array(dataX), numpy.array(dataY)
Si compara estas primeras 5 filas con la muestra del conjunto de datos original listada en la sección anterior, puede ver el patrón X=t e Y=t+1 en los números. Usemos esta función para preparar el tren y probar los conjuntos de datos listos para el modelado.
# remodelamos X=t y Y=t+1 look_back = 1 trainX, trainY = create_dataset(train, look_back) testX, testY = create_dataset(test, look_back)
Ahora podemos ajustar un modelo de Perceptron multicapa a los datos de entrenamiento. Usamos una red simple con 1 entrada, 1 capa oculta con 8 neuronas y una capa de salida. El modelo se ajusta utilizando el error cuadrático medio, si tomamos la raíz cuadrada nos da una puntuación de error en las unidades del conjunto de datos. Intenté algunos parámetros aproximados y establecí la configuración a continuación, pero de ninguna manera la red está optimizada.
# crear y adaptar el modelo Perceptron multicapa model = Sequential() model.add(Dense(8, input_dim=look_back, activation='relu')) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') model.fit(trainX, trainY, epochs=200, batch_size=2, verbose=2)
Una vez que el modelo es ajustado, podemos estimar el rendimiento del modelo en el entramiento y los conjuntos de datos de prueba. Esto nos dará un punto de comparación para los nuevos modelos.
# Estimacion del rendimiento del modelo
trainScore = model.evaluate(trainX, trainY, verbose=0)
print('Resultado del entrenamiento: %.2f MSE (%.2f RMSE)' % (trainScore, math.sqrt(trainScore)))
testScore = model.evaluate(testX, testY, verbose=0)
print('Resultado del test: %.2f MSE (%.2f RMSE)' % (testScore, math.sqrt(testScore)))
Finalmente, podemos generar predicciones utilizando el modelo tanto para el entrenamiento como para el conjunto de datos de prueba para obtener una indicación visual de la habilidad del modelo. Debido a cómo se preparó el conjunto de datos, debemos cambiar las predicciones para que se alineen en el eje x con el conjunto de datos original. Una vez preparados, se grafican los datos, mostrando el conjunto de datos original en azul, las predicciones para el conjunto de datos del entrenamiento en rojo y las predicciones sobre el conjunto de datos de prueba no visto en magenta.
# predicciones del entrenamiento generadas trainPredict = model.predict(trainX) testPredict = model.predict(testX) # predicciones del entrenamiento de cambio para plotear trainPredictPlot = numpy.empty_like(dataset) trainPredictPlot[:, :] = numpy.nan trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict # predicciones de la prueba de desplazamiento para plotear testPredictPlot = numpy.empty_like(dataset) testPredictPlot[:, :] = numpy.nan testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict # ploteamos la línea de base y las predicciones plt.plot(dataset) plt.plot(trainPredictPlot,'r', linewidth = 2) plt.plot(testPredictPlot,'m', linewidth = 2) plt.show()
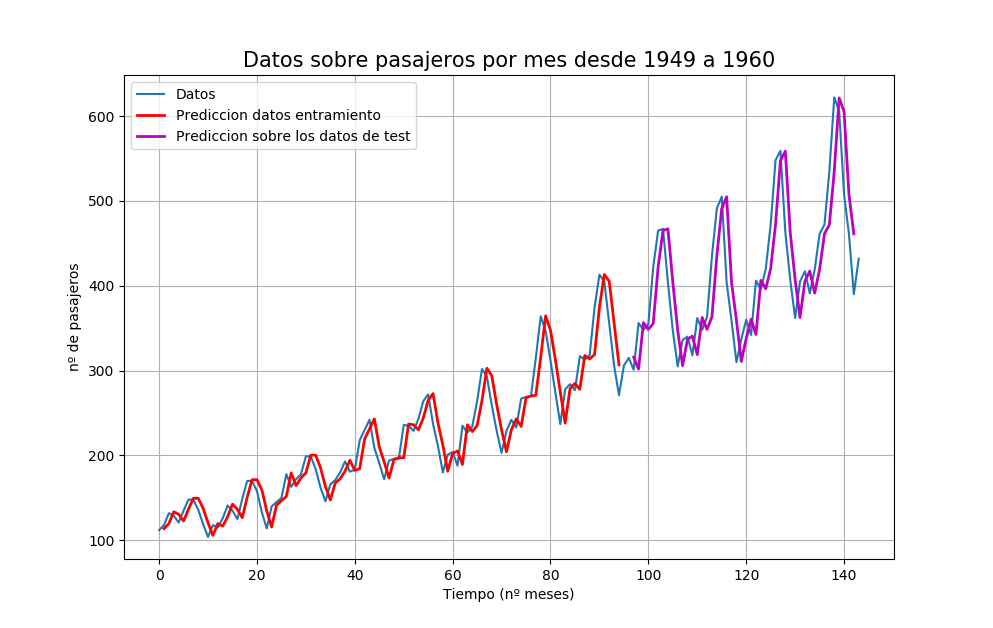
Podemos ver que el modelo hizo un trabajo bastante pobre en la evaluación de los conjuntos de datos de entrenamiento y de pruebas. Básicamente predijo el mismo valor de entrada que la salida. La gráfica hace que la predicción parezca buena, pero de hecho, el cambio en la predicción resulta en una puntuación de habilidad pobre.
# Perceptrón multicapa para predecir a los pasajeros de las aerolíneas internacionales (t+1, dado t)
import numpy
import matplotlib.pyplot as plt
from pandas import read_csv
import math
from keras.models import Sequential
from keras.layers import Dense
# convertimos un array de valores en una matriz de conjuntos de datos
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return numpy.array(dataX), numpy.array(dataY)
# semilla aleatoria para reproducibilidad
numpy.random.seed(7)
# cargamos el conjunto de datos
dataframe = read_csv('international-airline-passengers.csv', usecols=[1], engine='python',
skipfooter=3)
dataset = dataframe.values
dataset = dataset.astype('float32')
# dividimos entre entranmiento y test
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# remodelamos X=t y Y=t+1
look_back = 1
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# crear y ajuste el modelo Perceptron multicapa
model = Sequential()
model.add(Dense(8, input_dim=look_back, activation='relu'))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=200, batch_size=2, verbose=2)
# Estimacion del rendimiento del modelo
trainScore = model.evaluate(trainX, trainY, verbose=0)
print('Puntuacion de entrenamiento: %.2f MSE (%.2f RMSE)' % (trainScore, math.sqrt(trainScore)))
testScore = model.evaluate(testX, testY, verbose=0)
print('Puntuacion del test: %.2f MSE (%.2f RMSE)' % (testScore, math.sqrt(testScore)))
# generacion de prediccion para el entreno
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# predicciones del entrenamiento de cambio para plotear
trainPredictPlot = numpy.empty_like(dataset)
trainPredictPlot[:, :] = numpy.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# ploteamos linea base y predicciones
plt.plot(dataset)
plt.plot(trainPredictPlot,'r', linewidth = 2)
plt.plot(testPredictPlot,'m', linewidth = 2)
plt.legend( ('Datos', 'Prediccion datos entramiento', 'Prediccion sobre los datos de test'), loc = 'upper left')
plt.grid(True)
plt.title("Datos sobre pasajeros por mes desde 1949 a 1960", fontsize = 15)
plt.xlabel("Tiempo (nº meses)", fontsize = 10)
plt.ylabel("nº de pasajeros", fontsize = 10)
plt.show()
Corriendo el código podemos ver por consola:
Epoch 191/200 - 0s - loss: 537.5235 Epoch 192/200 - 0s - loss: 539.5366 Epoch 193/200 - 0s - loss: 546.4683 Epoch 194/200 .... Puntuacion de entrenamiento: 531.71 MSE (23.06 RMSE) Puntuacion del test: 2355.06 MSE (48.53 RMSE)
Tomando la raíz cuadrada de las estimaciones de rendimiento, podemos ver que el modelo tiene un error medio de 23 pasajeros (en miles) en el conjunto de datos de formación y 48 pasajeros (en miles) en el conjunto de datos de prueba.
Perceptrón multicapa por el método de la ventana
También podemos formular el problema de manera que se puedan utilizar múltiples pasos recientes para hacer la predicción para el próximo paso temporal. Esto se llama el método de la ventana, y el tamaño de la ventana es un parámetro que se puede ajustar para cada problema. Por ejemplo, dado el tiempo actual (t), nosotros queremos predecir el valor la próxima vez en la secuencia (t+1), podemos usar la hora actual (t) así como las dos veces anteriores (t-1 y t-2). Cuando se expresa como un problema de regresión, la las variables de entrada son t-2, t-1, t y la variable de salida es t+1.
La función create_dataset() que escribimos en la sección anterior nos permite crear la siguiente formulación del problema de las series temporales aumentando el argumento de look_back de 1 a 3 que tiene el siguiente aspecto:
X1 X2 X3 Y 112 118 132 129 118 132 129 121 132 129 121 135 129 121 135 148 121 135 148 148
Podemos volver a ejecutar el ejemplo de la sección anterior con el tamaño de ventana más grande. Aumentaremos la capacidad de la red para manejar la información adicional. La primera capa oculta se incrementa a 14 neuronas y se añade una segunda capa oculta con 8 neuronas. El número de épocas también aumenta a 400.
El listado completo del código con sólo el cambio de tamaño de la ventana se enumera a continuación para completarlo.
# Perceptrón multicapa para predecir a los pasajeros de las aerolíneas internacionales (t+1, dado t, t-1, t-2)
import numpy
import matplotlib.pyplot as plt
from pandas import read_csv
import math
from keras.models import Sequential
from keras.layers import Dense
# convertimos un array de valores en una matriz de conjuntos de datos
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return numpy.array(dataX), numpy.array(dataY)
# semilla aleatoria para reproducibilidad
numpy.random.seed(7)
# cargamos el conjunto de datos
dataframe = read_csv('international-airline-passengers.csv', usecols=[1], engine='python',skipfooter=3)
dataset = dataframe.values
dataset = dataset.astype('float32')
# dividimos entre entranmiento y test
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# remodelamos X=t y Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# crear y ajuste el modelo Perceptron multicapa
model = Sequential()
model.add(Dense(12, input_dim=look_back, activation='relu'))
model.add(Dense(8, activation='relu'))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=400, batch_size=2, verbose=2)
# Estimacion del rendimiento del modelo
trainScore = model.evaluate(trainX, trainY, verbose=0)
print('Puntuacion de entrenamiento: %.2f MSE (%.2f RMSE)' % (trainScore, math.sqrt(trainScore)))
testScore = model.evaluate(testX, testY, verbose=0)
print('Puntuacion del test: %.2f MSE (%.2f RMSE)' % (testScore, math.sqrt(testScore)))
# generacion de prediccion para el entreno
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# predicciones del entrenamiento de cambio para plotear
trainPredictPlot = numpy.empty_like(dataset)
trainPredictPlot[:, :] = numpy.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# predicciones del test de cambio para plotear
testPredictPlot = numpy.empty_like(dataset)
testPredictPlot[:, :] = numpy.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# ploteamos linea base y predicciones
plt.plot(dataset)
plt.plot(trainPredictPlot,'r', linewidth = 2)
plt.plot(testPredictPlot,'m', linewidth = 2)
plt.legend( ('Datos', 'Prediccion datos entramiento', 'Prediccion sobre los datos de test'), loc = 'upper left')
plt.grid(True)
plt.title("Datos sobre pasajeros por mes desde 1949 a 1960", fontsize = 15)
plt.xlabel("Tiempo (nº meses)", fontsize = 10)
plt.ylabel("nº de pasajeros", fontsize = 10)
plt.show()
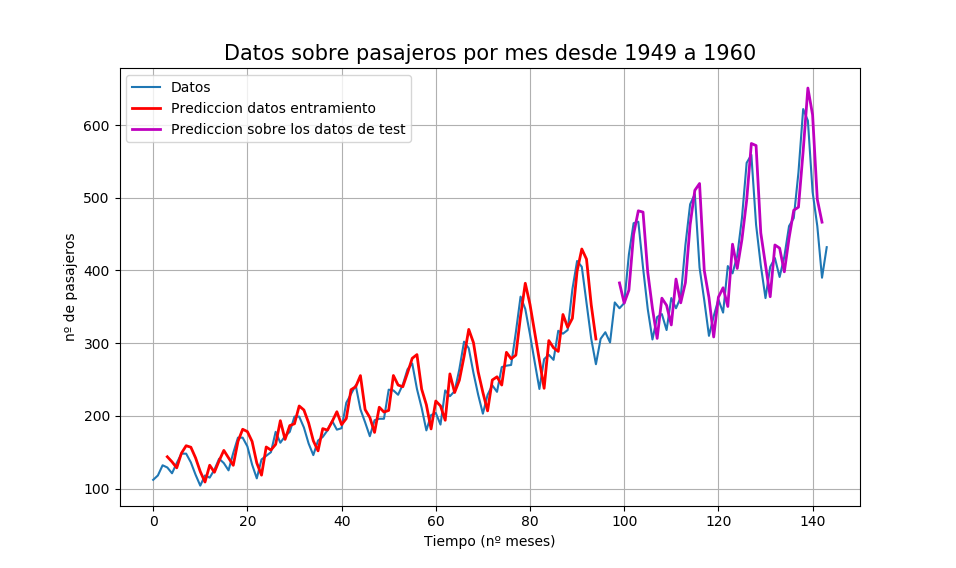
Cuando corremos el código obtenemos
Epoch 398/400 - 0s - loss: 479.8451 Epoch 399/400 - 0s - loss: 476.2427 Epoch 400/400 - 0s - loss: 489.4314 Puntuacion de entrenamiento: 565.12 MSE (23.77 RMSE) Puntuacion del test: 2233.80 MSE (47.26 RMSE)
Podemos ver que el error se redujo en comparación con el de la sección anterior. Una vez más, el tamaño de la ventana y la arquitectura de la red no fueron ajustados, esto es sólo una demostración de cómo enmarcar un problema de predicción. Tomando la raíz cuadrada de las puntuaciones de rendimiento podemos ver que el error medio en el conjunto de datos de entrenamiento fue de 23 pasajeros (en miles por mes) y el error medio en el conjunto de pruebas no visto fue de 47 pasajeros (en miles por mes).
➡ Aprende mucho mas de Deep Learning con nuestro curso:

[…] de las aerolíneas internacionales, el cual es un problema de predicción, descrito en el post anterior. Podemos decir que el problema es una regresión como se hizo en el capítulo anterior. Es decir, […]
Ejecuté tu código pero me surgió un error en : #Perceptrón multicapa para predecir a los pasajeros de las aerolíneas internacionales (t+1, dado t)
y no entiendo pues me dice que no están definidos amp;lt; amp;gt
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict</pre>
Podrás decirme ¿porqué?
Hola Car, ya esta arreglado. Gracias por comentar