Modelos MLP multivariantes (2/2)

Múltiples series paralelas

Un problema de series temporales alternativas es el caso cuando hay varias series temporales paralelas y una debe predecirse para cada uno de ellos. Por ejemplo, dados los datos de la sección anterior:

[[ 10 15 25]
[ 20 25 45]
[ 30 35 65]
[ 40 45 85]
[ 50 55 105]
[ 60 65 125]
[ 70 75 145]
[ 80 85 165]
[ 90 95 185]]

Es posible que queramos predecir el valor de cada una de las tres series temporales para el siguiente paso temporal. Este podría denominarse previsión multivariante. Una vez más, los datos deben dividirse en entrada/salida muestras para entrenar a una modelo. La primera muestra de este conjunto de datos sería:

Entrada:

10, 15, 25
20, 25, 45
30, 35, 65

Salida:

40, 45, 85

La función split_sequences() a continuación dividirá múltiples series temporales paralelas con filas para y una serie por columna en la forma de entrada/salida requerida.

# dividir una secuencia multivariante en muestras
def split_sequences(sequences, n_steps):
  X, y = list(), list()
  for i in range(len(sequences)):
    # encontrar el final de este patron
    end_ix = i + n_steps
    # comprobar si estamos mas alla del conjunto de datos
    if end_ix > len(sequences)-1:
     break
    # recoger las partes de entrada y salida del patron
    seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]
    X.append(seq_x)
    y.append(seq_y)
  return array(X), array(y)

Podemos demostrar esto en el problema creado; el ejemplo completo se enumera a continuación.

# preparacion de datos de salida multivariados
from numpy import array
from numpy import hstack
# dividir una secuencia multivariante en muestras
def split_sequences(sequences, n_steps):
  X, y = list(), list()
  for i in range(len(sequences)):
    # encuentra el final de este patron
    end_ix = i + n_steps
    # comprobar si estamos mas alla del conjunto de datos
    if end_ix > len(sequences)-1:
     break
    # recoger las partes de entrada y salida del patron
    seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]
    X.append(seq_x)
    y.append(seq_y)
  return array(X), array(y)
# definir la secuencia de entrada
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convertir a la estructura [rows, columns]
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# columnas aplicadas horizontalmente
dataset = hstack((in_seq1, in_seq2, out_seq))
# selecionar un numero de pasos de tiempo
n_steps = 3
# convertir en entrada/salida
X, y = split_sequences(dataset, n_steps)
print(X.shape, y.shape)
# resumir los datos
for i in range(len(X)):
  print(X[i], y[i])

Al ejecutar el ejemplo primero se imprime la forma de los componentes X e y preparados. El la forma de X es tridimensional, incluyendo el número de muestras (6), el número de pasos de tiempo elegido por muestra (3), y el número de series temporales o características paralelas (3). La forma de y es bidimensional, como cabría esperar para el número de muestras (6) y el número de tiempo variables por muestra que deben preverse (3). A continuación, se imprime cada una de las muestras mostrando la entrada y los componentes de salida de cada muestra.

(6, 3, 3) (6, 3)
[[10 15 25]
[20 25 45]
[30 35 65]] [40 45 85]
[[20 25 45]
[30 35 65]
[40 45 85]] [ 50 55 105]
[[ 30 35 65]
[ 40 45 85]
[ 50 55 105]] [ 60 65 125]
[[ 40 45 85]
[ 50 55 105]
[ 60 65 125]] [ 70 75 145]
[[ 50 55 105]
[ 60 65 125]
[ 70 75 145]] [ 80 85 165]
[[ 60 65 125]
[ 70 75 145]
[ 80 85 165]] [ 90 95 185]

Modelo MLP de salida vectorial

Ahora estamos listos para elaborar un modelo de MLP a partir de estos datos. Al igual que en el caso anterior de la multivariante de entrada, debemos la estructura tridimensional de las muestras de datos de entrada a un valor de dos estructura dimensional de [samples, features], donde las observaciones de retardo se tratan como características por el modelo.

# aplanar la entrada
n_input = X.shape[1] * X.shape[2]
X = X.reshape((X.shape[0], n_input))

El resultado del modelo será un vector, con un elemento para cada uno de los tres tiempos de diferenciación.

# determinar el numero se salidas
n_output = y.shape[1]

Ahora podemos rediseñar nuestro modelo, usando la directiva
longitud vectorial attened para la capa de entrada y el número de series temporales como la longitud del vector al hacer una predicción.

# definir modelo
model = Sequential()
model.add(Dense(100, activation='relu', input_dim=n_input))
model.add(Dense(n_output))
model.compile(optimizer='adam', loss='mse')

Podemos predecir el siguiente valor en cada una de las tres series paralelas proporcionando una entrada de tres pasos de tiempo para cada serie.

70, 75, 145
80, 85, 165
90, 95, 185

La forma de la entrada para hacer una sola predicción debe ser 1 muestra, 3 pasos de tiempo y 3 o [1, 3, 3, 3]. Una vez más, podemos aténgase a[1, 6] para satisfacer las expectativas del modelo. Esperamos que la salida vectorial sea:

[100, 105, 205]

# demostrar prediccion
x_input = array([[70,75,145], [80,85,165], [90,95,185]])
x_input = x_input.reshape((1, n_input))
yhat = model.predict(x_input, verbose=0)

Podemos relacionar todo esto y demostrar una MLP para series de tiempo de salida multivariadas.

# ejemplo de mlp de salida multivariada
from numpy import array
from numpy import hstack
from keras.models import Sequential
from keras.layers import Dense
# dividir una secuencia multivariante en muestras
def split_sequences(sequences, n_steps):
  X, y = list(), list()
  for i in range(len(sequences)):
    # encontran el final de este patron
    end_ix = i + n_steps
    # comprobar si estamos mas alla del conjuto de datos
    if end_ix > len(sequences)-1:
     break
    # recoger la parte de entrada y salida del patron
    seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]
    X.append(seq_x)
    y.append(seq_y)
  return array(X), array(y)
# definir la secuencia de entrada
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convertir a la estructura [rows, columns]
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# columnas aplicadas horizontalmente
dataset = hstack((in_seq1, in_seq2, out_seq))
# seleccionar un numero de pasos de tiempo
n_steps = 3
# convertir en entrada/salida
X, y = split_sequences(dataset, n_steps)
# aplanar entrada
n_input = X.shape[1] * X.shape[2]
X = X.reshape((X.shape[0], n_input))
n_output = y.shape[1]
# definir modelo
model = Sequential()
model.add(Dense(100, activation='relu', input_dim=n_input))
model.add(Dense(n_output))
model.compile(optimizer='adam', loss='mse')
# modelo aecuado
model.fit(X, y, epochs=2000, verbose=0)
# demostrar prediccion
x_input = array([[70,75,145], [80,85,165], [90,95,185]])
x_input = x_input.reshape((1, n_input))
yhat = model.predict(x_input, verbose=0)
print(yhat)

Ejecutando el ejemplo se preparan los datos, el modelo y se hace una predicción.

[[100.95039 107.541306 206.81033 ]]

Modelo MLP multi-salida

Al igual que con las series de entradas múltiples, existe otra forma más elaborada de modelar el problema. La serie de salida puede ser manejada por un modelo MLP de salida separado. Podemos referirnos a esto como un modelo MLP multi-salida. Puede ofrecer más de la calidad o de un mejor rendimiento en función de las especificaciones del problema que se está modelando. Este tipo de modelo puede ser denotado en Keras utilizando la API funcional de Keras. En primer lugar, podemos definir el modelo de entrada como un MLP con una entrada capa que espera vectores de característica atenuada.

# definir modelo
visible = Input(shape=(n_input,))
dense = Dense(100, activation='relu')(visible)

A continuación, podemos crear una capa de salida para cada una de las tres series que deseamos pronosticar, donde cada submodelo de salida pronosticará un solo paso temporal.

# definir salida 1
output1 = Dense(1)(dense)
# definir salida 2
output2 = Dense(1)(dense)
# definir salida 3
output3 = Dense(1)(dense)

Entonces podemos unir las capas de entrada y salida en un solo modelo.

# atar juntos
model = Model(inputs=visible, outputs=[output1, output2, output3])
model.compile(optimizer='adam', loss='mse')

Para aclarar la arquitectura del modelo, el siguiente esquema muestra claramente los tres elementos separados capas de salida del modelo y las formas de entrada y salida de cada capa.

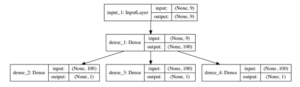
Cuando se entrene el modelo, se necesitarán tres matrices de salida separadas por muestras. Podemos lograr esto convirtiendo los datos de entrenamiento de salida que tienen la forma[7, 3] en tres matrices con la forma[7, 1].

# salida separada
y1 = y[:, 0].reshape((y.shape[0], 1))
y2 = y[:, 1].reshape((y.shape[0], 1))
y3 = y[:, 2].reshape((y.shape[0], 1))

Estas matrices se pueden proporcionar al modelo durante la formación.

# modelo de ajuste
model.fit(X, [y1,y2,y3], epochs=2000, verbose=0)

Enlazando todo esto, el ejemplo completo se muestra a continuación.

# ejemplo de mlp de salida multivariado
from numpy import array
from numpy import hstack
from keras.models import Model
from keras.layers import Input
from keras.layers import Dense
# dividir una secuencia multivariante en muestra
def split_sequences(sequences, n_steps):
  X, y = list(), list()
  for i in range(len(sequences)):
    # encontrar el final de este patron
    end_ix = i + n_steps
    # comprobar si estamos mas alla del conjunto de datos
    if end_ix > len(sequences)-1:
     break
    # recoger las partes de entrada y salida del patron
    seq_x, seq_y = sequences[i:end_ix, :], sequences[end_ix, :]
    X.append(seq_x)
    y.append(seq_y)
  return array(X), array(y)
# definir secuencia de entrada
in_seq1 = array([10, 20, 30, 40, 50, 60, 70, 80, 90])
in_seq2 = array([15, 25, 35, 45, 55, 65, 75, 85, 95])
out_seq = array([in_seq1[i]+in_seq2[i] for i in range(len(in_seq1))])
# convertir a estructura [rows, columns]
in_seq1 = in_seq1.reshape((len(in_seq1), 1))
in_seq2 = in_seq2.reshape((len(in_seq2), 1))
out_seq = out_seq.reshape((len(out_seq), 1))
# columnas apiladas horizontalmente
dataset = hstack((in_seq1, in_seq2, out_seq))
# seleccionar un numero de pasos de tiempo
n_steps = 3
# convertir en entrada/salida
X, y = split_sequences(dataset, n_steps)
# aplanar entrada
n_input = X.shape[1] * X.shape[2]
X = X.reshape((X.shape[0], n_input))
# salida separada
y1 = y[:, 0].reshape((y.shape[0], 1))
y2 = y[:, 1].reshape((y.shape[0], 1))
y3 = y[:, 2].reshape((y.shape[0], 1))
# definir modelo
visible = Input(shape=(n_input,))
dense = Dense(100, activation='relu')(visible)
# definir salida 1
output1 = Dense(1)(dense)
# definir salida 2
output2 = Dense(1)(dense)
# definir salida 13
output3 = Dense(1)(dense)
# unir
model = Model(inputs=visible, outputs=[output1, output2, output3])
model.compile(optimizer='adam', loss='mse')
# modelo de ajuste
model.fit(X, [y1,y2,y3], epochs=2000, verbose=0)
# demostrar prediccion
x_input = array([[70,75,145], [80,85,165], [90,95,185]])
x_input = x_input.reshape((1, n_input))
yhat = model.predict(x_input, verbose=0)
print(yhat)

Ejecutando el ejemplo se preparan los datos, el modelo y se hace una predicción.

[array([[100.86121]], dtype=float32),
array([[105.14738]], dtype=float32),
array([[205.97507]], dtype=float32)]