Blog
La ley de Coulomb, o ley inversa-cuadrada de Coulomb, es una ley de la física que describe la fuerza que interactúa entre las partículas estáticas cargadas eléctricamente. En su forma escalar, la ley es:
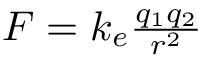
Donde ke es la constante de Coulomb (ke = 8.99×109 N m2 C−2), q1 y q2 son las magnitudes firmadas de las cargas, y el escalar r es la distancia entre las cargas. La fuerza de interacción entre las cargas es atractiva si las cargas tienen signos opuestos (es decir, F es negativa) y repulsiva si están firmadas de igual manera (es decir, F es positiva).
La ley fue publicada por primera vez en 1784 por el físico francés Charles-Augustin de Coulomb y fue esencial para el desarrollo de la teoría del electromagnetismo. Siendo una ley inversa-cuadrada, es análoga a la ley inversa-cuadrada de Isaac Newton de la gravitación universal. La ley de Coulomb puede ser usada para derivar la ley de Gauss, y viceversa. La ley ha sido probada extensamente, y todas las observaciones han confirmado el principio de la ley.
Ejemplos:
Ejemplo 1: Una carga de 3×10^-6 C se encuentra 2 m de una carga de -8×10^-6 C, ¿Cuál es la magnitud de la fuerza de atracción entre las cargas?
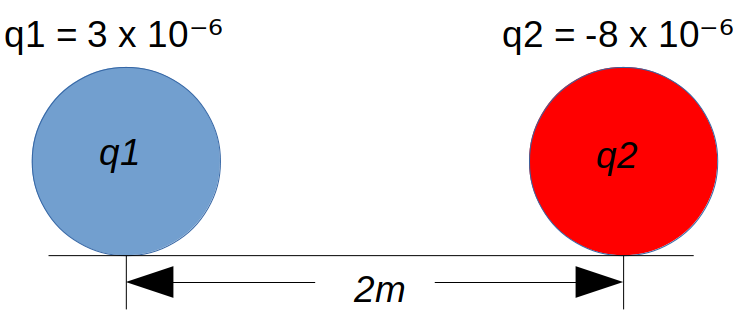
Una forma de resolver este problema con un programa escrito en Python sería:
def fuerza(q1:float,q2:float,r:float) -> float: # Se define una función que recibe como entrada las cargas y la distancia y devuelve la fuerza
k = (8.99)*(10**9) # Se define el valor de la constante de Coulomb
return (k*q1*q1)/(r**2) # El valor de retorno será la aplicación de la formula
q1 = 3*(10**(-6)) # Valor de la primera carga
q2 = -8*(10**(-6)) # Valor de la segunda carga
r = 2.0 # Distancia entre las dos cargas
print("El valor de la fuerza de atracción entre las dos cargas es: " + str(fuerza(q1,q2,r)))
De forma mas general, se puede definir un programa que reciba como entrada el valor de las cargas y de la distancia entre ambas y calcule la fuerza de atracción entre ellas. Esto sería:
def fuerza(q1:float,q2:float,r:float) -> float:
k = (8.99)*(10**9)
return (k*q1*q1)/(r**2)
q1 = float(input("Ingrese el valor de la primera carga\n"))
q2 = float(input("Ingrese el valor de la segunda carga\n"))
r = float(input("Ingrese el valor de la distancia ente ambas cargas\n"))
print("El valor de la fuerza de atracción entre las dos cargas es: " + str(fuerza(q1,q2,r)))
El resultado es: -0.054 N
Ejemplo 2: Una carga de -5×10^-7 C ejerce una fuerza a otra carga de 0.237 N a una distancia de 3.5 metros, ¿cuál es el valor de la segunda carga?
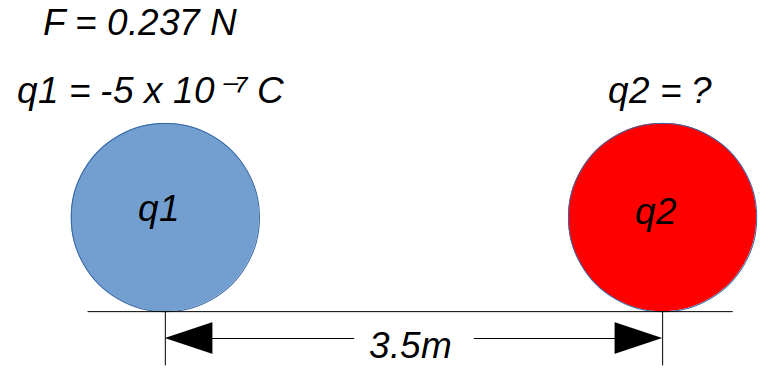
De forma similar, se definirá una función que calcule el valor de la carga, utilizando la fórmula de coulomb, despejando el valor de la carga:
El despeje sería:
![]()
El programa sería:
def carga(f:float,q:float,r:float) -> float: # Función que calcula el valor de la carga faltante recibiendo el valor de la fuerza, la distancia y la otra carga
k = (8.99)*(10**9) # Constante de Coulomb
return (f*(r**2))/(q*k) # Aplicación de la formula
f = 0.237 # Valor de la fuerza
q1 = (-5)*(10**(-7)) # Valor de la carga
r = 3.5 # Distancia entre ambas cargas
print("El valor de la carga es: " + str(carga(f,q1,r)))
Se puede crear una versión mas general del programa que tome los valores de la fuerza, la carga y la distancia como entrada y calcule el valor de la carga. Esto sería:
def carga(f:float,q:float,r:float) -> float:
k = (8.99)*(10**9)
return (f*(r**2))/(q*k)
f = float(input("Ingrese el valor de la fuerza\n"))
q1 = float(input("Ingrese el valor de la carga\n"))
r = float(input("Ingrese la distancia entre ambas cargas\n"))
print("El valor de la carga es: " + str(carga(f,q1,r)))
El resultado es: -0.644×10^-3 C
Ejemplo 3: Dos cargas con 2.8×10^-6 C y 7.5×10^-6 C respectivamente se atraen con una fuerza de 10N, ¿A qué distancia se encuentran separadas?
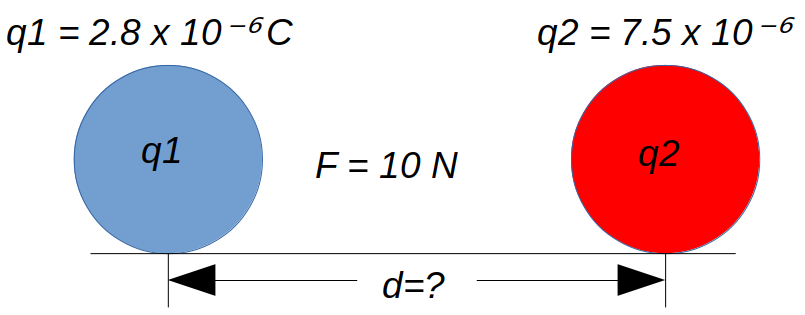
Con un programa similar al de los ejemplos anteriores, se puede resolver este ejercicio, tomando en cuenta el despeje pertinente de la formula de la ley de Coulomb. Esto sería:
El despeje sería:
El programa sería:
def sqrt(x) -> float: # Funcion para calcular la raiz cuadrada de un numero
return x**(1/2)
def distancia(q1:float,q2:float,f:float) -> float: # Funcion para calcular la distancia entre dos cargas
k = (8.99)*(10**9) # Constante de Coulomb
return sqrt((k*q1*q2)/f) # Aplicación de la formula de Coulomb con su despeje
q1 = 2.8 * (10**(-6)) # Valor de la primera carga
q2 = 7.5 * (10**(-6)) # Valor de la segunda carga
f = 10.0 # Valor de la fuerza
print("La distancia entre ambas cargas es: " + str(distancia(q1,q2,f)))
En este ejercicio se definió la función para calcular la raíz cuadrada de un numero porque esta sería necesaria para calcular el resultado del problema.
Una versión mas general del problema que reciba los valores de las cargas y de la fuerza como entrada sería:
def sqrt(x) -> float:
return x**(1/2)
def distancia(q1:float,q2:float,f:float) -> float:
k = (8.99)*(10**9) # Constante de Coulomb
return sqrt((k*q1*q2)/f) # Aplicación de la formula de Coulomb con su despeje
q1 = float(input("Ingrese el valor de la primera carga\n"))
q2 = float(input("Ingrese el valor de la segunda carga\n"))
f = float(input("Ingrese el valor de la fuerza\n"))
print("La distancia entre ambas cargas es: " + str(distancia(q1,q2,f)))
El resultado es d = 0.1374 m
Historia de la ley de Coulomb
Las culturas antiguas alrededor del Mediterráneo sabían que ciertos objetos, como varillas de ámbar, podían ser frotados con el pelo de gato para atraer objetos ligeros como plumas. Thales of Miletus hizo una serie de observaciones sobre la electricidad estática alrededor del año 600 a. C., a partir de las cuales creyó que la fricción hacía al ámbar magnético, en contraste con minerales como la magnetita, que no necesitaba frotarse. Thales estaba equivocado al creer que la atracción se debía a un efecto magnético, pero más tarde la ciencia probaría un vínculo entre el magnetismo y la electricidad. La electricidad seguiría siendo poco más que una curiosidad intelectual durante milenios hasta 1600, cuando el científico inglés William Gilbert hizo un estudio cuidadoso de la electricidad y el magnetismo, distinguiendo el efecto lodestone de la electricidad estática producida por el roce del ámbar. Él acuñó la nueva palabra latina electricus para referirse a la propiedad de atraer objetos pequeños después de ser frotado. Esta asociación dio origen a las palabras inglesas “electric” y “electricity”, que hicieron su primera aparición en imprenta en la Pseudodoxia Epidemica de Thomas Browne de 1646.
Los primeros investigadores del siglo XVIII que sospechaban que la fuerza eléctrica disminuyó con la distancia como la fuerza de gravedad (es decir, como el cuadrado inverso de la distancia) incluyeron a Daniel Bernoulli y Alessandro Volta, que midieron la fuerza entre las placas de un condensador, y Franz Aepinus que supuso la ley del cuadrado inverso en 1758.
Basado en experimentos con esferas cargadas eléctricamente, Joseph Priestley de Inglaterra fue uno de los primeros en proponer que la fuerza eléctrica seguía una ley de cuadrado inverso, similar a la ley de gravitación universal de Newton. Sin embargo, no generalizó ni profundizó en esto. En 1767, conjeturó que la fuerza entre cargas variaba como el cuadrado inverso de la distancia.
En 1769, el físico escocés John Robison anunció que, según sus mediciones, la fuerza de repulsión entre dos esferas con cargas del mismo signo variaba como x−2.06.
A principios de la década de 1770, Henry Cavendish de Inglaterra ya había descubierto, pero no publicado, la dependencia de la fuerza entre los cuerpos acusados tanto de distancia como de cargo.
Finalmente, en 1785, el físico francés Charles-Augustin de Coulomb publicó sus tres primeros informes sobre la electricidad y el magnetismo en los que afirmaba su ley. Esta publicación fue esencial para el desarrollo de la teoría del electromagnetismo. Utilizó un balance de torsión para estudiar las fuerzas de repulsión y atracción de las partículas cargadas, y determinó que la magnitud de la fuerza eléctrica entre dos cargas puntuales es directamente proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia entre ellas.
El balance de torsión consiste en una barra suspendida desde su centro por una fibra fina. La fibra actúa como un resorte de torsión muy débil. En el experimento de Coulomb, la balanza de torsión era una varilla aislante con una bola metálica adherida a un extremo, suspendida por un hilo de seda. La bola fue cargada con una carga conocida de electricidad estática, y una segunda bola cargada de la misma polaridad se acercó a ella. Las dos bolas cargadas se repelían unas a otras, girando la fibra a través de un cierto ángulo, que se podía leer desde una escala en el instrumento. Sabiendo cuánta fuerza se necesitó para torcer la fibra a través de un ángulo dado, Coulomb fue capaz de calcular la fuerza entre las bolas y derivar su ley de proporcionalidad inversa-cuadrada.
La ley
La ley de Coulomb lo dice así:
La magnitud de la fuerza electrostática de atracción o repulsión entre dos cargas puntuales es directamente proporcional al producto de las magnitudes de cargas e inversamente proporcional al cuadrado de la distancia entre ellas.
La fuerza está a lo largo de la línea recta que los une. Si las dos cargas tienen el mismo signo, la fuerza electrostática entre ellas es repulsiva; si tienen signos diferentes, la fuerza entre ellas es atractiva.
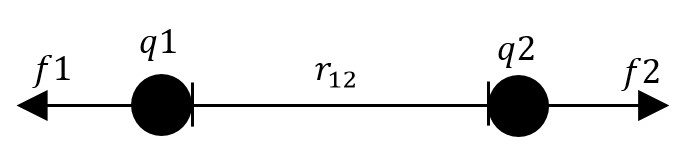
La ley de Coulomb también puede ser expresada como una simple expresión matemática. Las formas escalares y vectoriales de la ecuación matemática son:
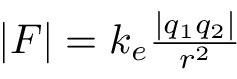 y
y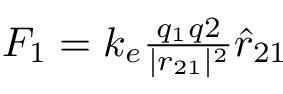 respectivamente,
respectivamente,
donde ke es la constante de Coulomb (ke = 8.9875517873681764×109 N m2 C−2), q1 y q2 son las magnitudes firmadas de las cargas, el escalar r es la distancia entre las cargas, el vector r21 = r1 − r2 es la distancia vectorial entre las cargas, y r̂21 = r21/|r21| (un vector unitario que apunta de q2 a q1). La forma vectorial de la ecuación calcula la fuerza F1 aplicada en q1 por q2. Si en su lugar se utiliza r12 se puede encontrar el efecto en q2. También puede calcularse utilizando la tercera ley de Newton: F2 = −F1.
Unidades
Cuando la teoría electromagnética se expresa utilizando las unidades SI estándar, la fuerza se mide en newtons, carga en Coulomb y distancia en metros. La constante de Coulomb viene dada por ke = 1⁄4πε0. La constante ε0 es la permitividad del espacio libre en C2 m−2 N−1. Y ε es la permitividad relativa del material en el que se sumergen las cargas, y no tiene dimensión.
Las unidades derivadas del SI para el campo eléctrico son voltios por metro, newtons por coulomb, o medidores tesla por segundo.
La ley de Coulomb y la constante de Coulomb también pueden interpretarse en varios términos:
- Unidades atómicas. En las unidades atómicas, la fuerza se expresa en hartrees por radio Bohr, la carga en términos de carga elemental y las distancias en términos del radio Bohr.
- Unidades electrostáticas o unidades gaussianas. En las unidades electrostáticas y unidades gaussianas, la carga unitaria (esu o statcoulomb) se define de tal manera que la constante k de Coulomb desaparece porque tiene el valor de una y se vuelve sin dimensión.
Las unidades CGS son a menudo preferidas en el tratamiento del electromagnetismo, ya que simplifican enormemente las fórmulas.
La constante de Coulomb
La constante de Coulomb es un factor de proporcionalidad que aparece en la ley de Coulomb, así como en otras fórmulas relacionadas con la electricidad. Denota ke, también se llama la constante de fuerza eléctrica o constante electrostática, de ahí el subíndice e.
El valor exacto de la constante de Coulomb es:
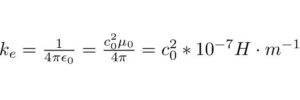
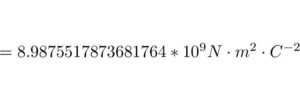
Condiciones de validez
Hay tres condiciones que deben cumplirse para la validez de la ley de Coulomb:
- Las cargas deben tener una distribución esférica simétrica (por ejemplo, cargas puntuales o una esfera metálica cargada).
- Las tasas no deben solaparse (p. ej., tasas por puntos distintas).
- Los cargos deben ser fijos entre sí.


excelente aporte…. sigan adelante… Gracias…
dos pequeñas esferas identicas de tecnopor cada una con 0.030 kg de masa cuelgan en quilibrio. si la longitud de cada hilo aislante es de 30cm y el angulo 0=7°