Blog
Importancia del sistema hexadecimal en Python
- Publicado por: Rafael Fernandez
- Categoría: Blog
Los sistemas de numeración son el conjunto de símbolos y reglas que se emplean para representar números y cantidades. Además del sistema decimal existe el binario, el octal y hexadecimal, cada uno caracterizado por su base, diez, dos, ocho y dieciséis respectivamente.
En esta ocasión hablaremos del sistema hexadecimal (16); los símbolos que la representan, su utilidad en el mundo de la informática y como realizar la conversión mediante el lenguaje de programación Python.
El sistema hexadecimal
Es el sistema de numeración de base 16. Esta representado por los 10 números del sistema decimal y las primeras 6 letras del alfabeto (A, B, C, D, E, F).
S16 = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}
Importante en la informática
En el ámbito informático el sistema hexadecimal resulta muy ventajoso debido a que cada digito hexadecimal equivale a 4 dígitos binarios. Por lo tanto, 2 dígitos hexadecimales representan una unida básica de almacenamiento de información (8bits – 1byte), mientras que en binarios serían 4 dígitos.
En palabras más simples, este sistema de numeración tiene la capacidad de simplificar valores de datos e instrucciones de memoria.
Es por esta razón que los microordenadores utilizan este sistema, pues permiten acortar largas series de unos y ceros, haciendo que la transportación de datos e información se realice de forma más rápida y eficiente.
Conversión manual
Convertir números binarios en hexadecimales y viceversa es bastante sencillo, solo debemos seguir los siguientes pasos:
De binario a hexadecimal
Explicaremos el procedimiento de conversión con un ejemplo práctico.
El siguiente número binario 110010101001101101 2 lo convertiremos en hexadecimal.
Paso 1: Crear plantilla
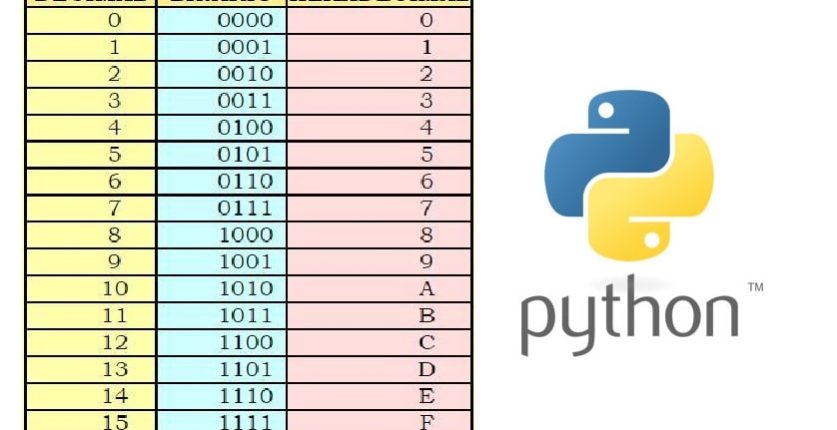
Para realizar la conversión necesitaremos la tabla de equivalencias entre el sistema binario y hexadecimal.
| Binario | Hexadecimal |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Paso2: Agrupar
Dividir el número en grupos de cuatro dígitos comenzando en el lado derecho.
11-0010-1010-0110-1101
Paso 3: Completar
Si quedan algunos dígitos sin agrupar como sucede en este caso, los completamos con ceros a la izquierda.
0011-0010-1010-0110-1101
Paso 4: Buscar equivalencia
El último paso es convertir cada grupo de dígitos basándonos en la plantilla del paso 1.
De manera que:
1101 = D
0110 = 6
1010 = A
0010 = 2
0011 = 3
Por lo tanto, el número binario 110010101001101101 2 equivale al número hexadecimal 32A6D 16.
De hexadecimal a binario
Para hacer la conversión del sistema hexadecimal a binario realizamos el mismo procedimiento, pero a la inversa.
Es decir, teniendo en cuenta la plantilla de conversión, buscamos el equivalente binario de cada digito hexadecimal.
A continuación, realizaremos el procedimiento utilizando el ejemplo anterior:
Valor hexadecimal: 32A6D 16
D = 1101
6 = 0110
A = 1010
2 = 0010
3 = 0011
Valor binario: 00110010101001101101 2
Métodos y Bibliotecas Python
Como hemos visto resulta muy sencillo realizar la conversión manual entre estos sistemas de numeración. No obstante, para casos de conversión masiva puede volver una tarea bastante tediosa.
Afortunadamente, Python cuenta con el método “int” y la biblioteca “base64”.
Método INT
Sintaxis: int(‘numero a convertir’, base del sistema numérico)
Básicamente lo que hace es convertir a sistema decimal el número binario, octal o hexadecimal que hayamos elegido.
Por ejemplo:
SBin = int('101001011', 2) # De Binario a Decimal
print(SBin) # Resultado: 331
SHex = int('A47F2', 16) # De Hexadecimal a Decimal es base usada por el sistema hexadecimal
print(SHex) # Resultado: 673778
SOct = int('731254', 8) # De octal a Decimal
print(SOct) # Resultado: 242348
Librería base64
Mediante esta librería es posible codificar y decodificar datos numéricos a caracteres ASCII o viceversa.
Ahora bien, aunque existen distintos tipos de codificaciones que podemos realizar con el módulo base 64, en este artículo hablaremos de aquel que nos proporciona la codificación y decodificación hexadecimal.
Para ello debemos en primer lugar importarla y luego usar la sintaxis correspondiente, tal como mostramos en el siguiente código:
import base64 python64 = base64.b16encode (b'Dato que queremos decodificar') print(python64) #Muestra como resultado b'4461746F207175652071756572656D6F73206465636F64696669636172' python = base64.b16decode (python64) print(python) # Muestra b'Dato que queremos decodificar'
Tal como se muestra en el ejemplo es posible decodificar cadenas de texto a su equivalente hexadecimal.
Recordemos que su utilidad es simplificar el envío de información y aunque no lo vemos palpable debemos recordar que, en binario esta misma cadena de caracteres equivale a 4 veces la longitud. Por lo tanto, resulta útil realizar la conversión.
Conversión automatizada con Python
Ahora aprenderemos a realizar nuestro propio conversor con Python. Haremos que al introducir un número decimal lo presente en su equivalente hexadecimal.
def Conversor(): # Función principal
decimal = int(input("Introduzca un numero positivo para convertirlo a hexodecimal: ")) # Solicitud al usuario para que introduzca un decimal
hexadecimal = ""
while decimal != 0:
rem = CambiarDigitos(decimal % 16) # Divide entre 16 y guarda el resto
hexadecimal = str(rem) + hexadecimal
decimal = int(decimal / 16)
print("Resultado: " + hexadecimal)
def CambiarDigitos(digitos): # Convierte cada digito en su equivalencia hexadecimal
decimales = [10 , 11 , 12 , 13 , 14 , 15 ]
hexadecimal = ["A", "B", "C", "D", "E", "F"]
for c in range(7):
if digitos == decimales[c - 1]:
digitos = hexadecimal[c - 1]
return digitos
Conversor()
