Flujo óptico Lucas-Kanade y Gunner Farneback

Flujo óptico

El flujo óptico es el patrón de movimiento aparente de los objetos de la imagen entre dos fotogramas consecutivos causado por el movimiento del objeto o la cámara. Es un campo vectorial 2D donde cada vector es un vector de desplazamiento que muestra el movimiento de los puntos del primer cuadro al segundo. Considere la imagen de abajo.

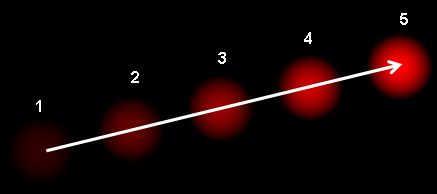
Muestra una bola moviéndose en 5 cuadros consecutivos. La flecha muestra su vector de desplazamiento. El flujo óptico tiene muchas aplicaciones en áreas como:

• Estructura desde el movimiento
• Compresión de vídeo
• Estabilización de vídeo…

El flujo óptico trabaja sobre varios supuestos:

1. Las intensidades de píxel de un objeto no cambian entre fotogramas consecutivos.
2. Los píxeles vecinos tienen movimiento similar.

Considere un píxel I (x, y, t) en el primer cuadro (Consulte una nueva dimensión, el tiempo, se agrega aquí. Antes sólo trabajábamos con imágenes, así que no necesitábamos tiempo). Se mueve por distancia (dx, dy) en el siguiente cuadro tomado después del tiempo dt. Así que como esos píxeles son los mismos y la intensidad no cambia, podemos decir,

I (x, y, t) = I (x+dx, y+dy, t+dt)

A continuación, realice la aproximación de la serie taylor del lado derecho, elimine los términos comunes y divida por dt para obtener la siguiente ecuación:

f_x u + f_y v + f_t = 0

donde:

La ecuación anterior se llama ecuación de flujo óptico. En ella podemos encontrar f_x y f_y, son gradientes de imagen. Del mismo modo f_t es el gradiente a lo largo del tiempo. Pero (u, v) es desconocido. No podemos resolver esta ecuación con dos variables desconocidas. Así que se proporcionan varios métodos para resolver este problema y uno de ellos es Lucas-Kanade.

Método Lucas-Kanade

Hemos visto una suposición anterior de que todos los píxeles vecinos tendrán un movimiento similar. El método Lucas-Kanade toma un parche de 3×3 alrededor del punto. Así que todos los 9 puntos tienen la misma moción. Podemos encontrar (f_x, f_y, f_t) para estos 9 puntos. Así que ahora nuestro problema se convierte en resolver 9 ecuaciones con dos variables desconocidas que están sobredeterminadas. Se obtiene una mejor solución con el método de ajuste cuadrado. Abajo está la solución final que son dos ecuaciones.

(Compruebe la similitud de la matriz inversa con el detector de esquinas Harris. Denota que las curvas son mejores puntos a ser rastreados.

Así que desde el punto de vista del usuario, la idea es simple, damos algunos puntos a rastrear, recibimos los vectores de flujo óptico de esos puntos. Pero de nuevo hay algunos problemas. Hasta ahora, nos ocupábamos de pequeños movimientos. Así que falla cuando hay movimiento grande. Así que otra vez vamos por las pirámides. Cuando subimos en la pirámide, los movimientos pequeños son removidos y los movimientos grandes se convierten en movimientos pequeños. Aplicando Lucas-Kanade, tenemos flujo óptico junto con la escala.

Ejemplo Flujo óptico Lucas-Kanade en OpenCV

OpenCV proporciona todo esto en una sola función, cv2.calcOpticalFlowPyrLK(). Aquí creamos una aplicación sencilla que rastrea algunos puntos en un vídeo. Para decidir los puntos, utilizamos cv2.goodFeaturesToTrack(). Tomamos el primer fotograma, detectamos algunos puntos de esquina Shi-Tomasi en él, luego hacemos un seguimiento iterativo de esos puntos usando el flujo óptico Lucas-Kanade. Para la función cv2.calcOpticalFlowPyrLK () pasamos el fotograma anterior, los puntos anteriores y el fotograma siguiente. Devuelve los siguientes puntos junto con algunos números de estado que tienen un valor de 1 si se encuentra el siguiente punto, o bien cero. Pasamos de manera iterativa estos próximos puntos como puntos anteriores en el próximo paso. Vea el código abajo:

import numpy as np
import cv2

cap = cv2.VideoCapture('toki.mp4')
# parametros para detección de esquinas ShiTomasi
feature_params = dict( maxCorners = 100,
                       qualityLevel = 0.3,
                       minDistance = 7,
                       blockSize = 7 )

# Parámetros para el flujo óptico de Lucas Kanade
lk_params = dict( winSize = (15,15),
                  maxLevel = 2,
                  criteria = (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 0.03))

# Crea algunos colores aleatorios
color = np.random.randint(0,255,(100,3))
# Toma el primer cuadro y encuentra esquinas en él
ret, old_frame = cap.read()
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
p0 = cv2.goodFeaturesToTrack(old_gray, mask = None, **feature_params)

# Crear una máscara de imagen para dibujar
mask = np.zeros_like(old_frame)

while(1):
  ret,frame = cap.read()
  frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

  # calcula optical flow
  p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)

  # Select good points
  good_new = p1[st==1]
  good_old = p0[st==1]

  # dibuja las lineas
  for i,(new,old) in enumerate(zip(good_new,good_old)):
    a,b = new.ravel()
    c,d = old.ravel()
    mask = cv2.line(mask, (a,b),(c,d), color[i].tolist(), 2)
    frame = cv2.circle(frame,(a,b),5,color[i].tolist(),-1)
  img = cv2.add(frame,mask)

  cv2.imshow('frame',img)
  k = cv2.waitKey(30) & 0xff
  if k == 27:
    break

  # Ahora actualiza el marco anterior y los puntos anteriores
  old_gray = frame_gray.copy()
  p0 = good_new.reshape(-1,1,2)

cv2.destroyAllWindows()
cap.release()

(Este código no verifica cuán correctos son los siguientes puntos clave. Por lo tanto, incluso si cualquier punto de característica desaparece en la imagen, existe la posibilidad de que el flujo óptico encuentre el siguiente punto que pueda mirarlo de cerca. Así que para un seguimiento robusto, los puntos de esquina deben ser detectados en intervalos particulares. Las muestras de OpenCV vienen con una muestra que encuentra los puntos de característica en cada 5 fotogramas. También ejecuta una comprobación hacia atrás de los puntos de flujo ópticos, que sólo tienen que seleccionar los buenos).

Vea los resultados que tenemos:

Flujo óptico denso Gunner Farneback en OpenCV

El método Lucas-Kanade calcula el flujo óptico para un conjunto de características dispersas (en nuestro ejemplo, las esquinas detectadas mediante el algoritmo Shi-Tomasi). OpenCV proporciona otro algoritmo para encontrar el flujo óptico denso. Calcula el flujo óptico para todos los puntos del cuadro. Se basa en el algoritmo de Gunner Farneback, que se explica en “Two-Frame Motion Estimmation Based on Polynomial Expansion” de Gunner Farneback en 2003.

A continuación se muestra cómo encontrar el flujo óptico denso utilizando el algoritmo anterior. Obtenemos una matriz de 2 canales con vectores de flujo óptico, (u, v). Encontramos su magnitud y dirección. Coloreamos el resultado para una mejor visualización. La dirección corresponde al valor Hue de la imagen. La Magnitud corresponde al Plano de Valor. Vea el código abajo:

import cv2
import numpy as np
cap = cv2.VideoCapture("toki.mp4")

ret, frame1 = cap.read()
prvs = cv2.cvtColor(frame1,cv2.COLOR_BGR2GRAY)
hsv = np.zeros_like(frame1)
hsv[...,1] = 255

while(1):
  ret, frame2 = cap.read()
  next = cv2.cvtColor(frame2,cv2.COLOR_BGR2GRAY)

  flow = cv2.calcOpticalFlowFarneback(prvs,next, None, 0.5, 3, 15, 3, 5, 1.2, 0)

  mag, ang = cv2.cartToPolar(flow[...,0], flow[...,1])
  hsv[...,0] = ang*180/np.pi/2
  hsv[...,2] = cv2.normalize(mag,None,0,255,cv2.NORM_MINMAX)
  rgb = cv2.cvtColor(hsv,cv2.COLOR_HSV2BGR)

  cv2.imshow('frame2',rgb)
  k = cv2.waitKey(30) & 0xff
  if k == 27:
    break
  elif k == ord('s'):
    cv2.imwrite('opticalfb.png',frame2)
    cv2.imwrite('opticalhsv.png',rgb)
  prvs = next

cap.release()
cv2.destroyAllWindows()