Blog
El principio de Bernoulli y ejercicios con Python
- Publicado por: Rafael Fernandez
- Categoría: Blog

En la dinámica de fluidos, el principio de Bernoulli establece que un aumento en la velocidad de un fluido ocurre simultáneamente con una disminución en la presión o una disminución en la energía potencial del fluido. El principio lleva el nombre de Daniel Bernoulli que lo publicó en su libro Hydrodynamica en 1738.
El principio de Bernoulli se puede aplicar a varios tipos de flujo de fluido, resultando en varias formas de la ecuación de Bernoulli; hay diferentes formas de la ecuación de Bernoulli para diferentes tipos de flujo. La forma simple de la ecuación de Bernoulli es válida para flujos incompresibles (por ejemplo, la mayoría de los flujos de líquidos y gases que se mueven a un número Mach bajo). Se pueden aplicar formas más avanzadas a flujos compresibles con números Mach más altos (ver las derivaciones de la ecuación de Bernoulli).
El principio de Bernoulli puede derivarse del principio de conservación de la energía. Esto indica que, en un flujo constante, la suma de todas las formas de energía en un fluido a lo largo de una línea de corriente es la misma en todos los puntos de esa línea de corriente. Esto requiere que la suma de energía cinética, energía potencial y energía interna permanezca constante. Así pues, un aumento en la velocidad del fluido – lo que implica un aumento tanto de su presión dinámica como de su energía cinética – se produce con una disminución simultánea en (la suma de) su presión estática, energía potencial y energía interna. Si el fluido fluye fuera de un depósito, la suma de todas las formas de energía es la misma en todas las líneas de flujo, porque en un depósito la energía por unidad de volumen (la suma de presión y potencial gravitacional ρ g h) es la misma en todas partes.
El principio de Bernoulli también puede derivarse directamente de la Segunda Ley del Movimiento de Isaac Newton. Si un pequeño volumen de fluido fluye horizontalmente desde una región de alta presión a una región de baja presión, entonces hay más presión detrás que delante. Esto da una fuerza neta sobre el volumen, acelerándolo a lo largo de la línea aerodinámica.
Las partículas fluidas sólo están sujetas a presión y a su propio peso. Si un fluido está fluyendo horizontalmente y a lo largo de una sección de una línea aerodinámica, donde la velocidad aumenta sólo puede ser porque el fluido en esa sección se ha movido de una región de presión más alta a una región de presión más baja; y si su velocidad disminuye, sólo puede ser porque se ha movido de una región de presión más baja a una región de presión más alta. Consecuentemente, dentro de un fluido que fluye horizontalmente, la velocidad más alta ocurre donde la presión es más baja, y la velocidad más baja ocurre donde la presión es más alta.
Ecuación de caudal incompresible
En la mayoría de los flujos de líquidos, y de gases con un número Mach bajo, la densidad de una parcela de fluido puede considerarse constante, independientemente de las variaciones de presión en el flujo. Por lo tanto, el fluido puede considerarse incompresible y estos flujos se denominan flujos incompresibles. Bernoulli realizó sus experimentos con líquidos, por lo que su ecuación en su forma original es válida sólo para un flujo incompresible. Una forma común de la ecuación de Bernoulli, válida en cualquier punto arbitrario a lo largo de una línea aerodinámica, es:
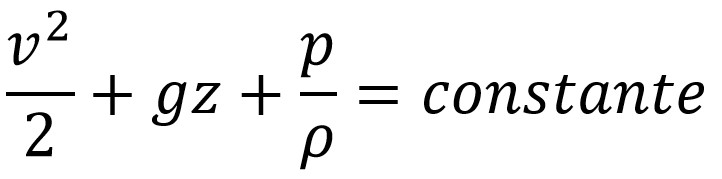
donde:
- v es la velocidad de flujo del fluido en un punto de una línea aerodinámica,
- g es la aceleración debida a la gravedad,
- z es la elevación del punto por encima de un plano de referencia, con la dirección z positiva apuntando hacia arriba, es decir, en la dirección opuesta a la aceleración gravitacional,
- p es la presión en el punto elegido, y
- p es la densidad del fluido en todos los puntos del fluido.
La constante en el lado derecho de la ecuación depende sólo de la aerodinámica elegida, mientras que v, z y p dependen del punto particular de esa aerodinámica.
Para que se aplique esta ecuación de Bernoulli deben cumplirse los siguientes supuestos:
- El caudal debe ser estable, es decir, las propiedades del fluido (velocidad, densidad, etc…) en un punto no pueden cambiar con el tiempo,
- El caudal debe ser incompresible – aunque la presión varíe, la densidad debe permanecer constante a lo largo de una línea aerodinámica;
- La fricción por fuerzas viscosas tiene que ser insignificante.
Para los campos de fuerza conservadores (no limitados al campo gravitacional), la ecuación de Bernoulli puede generalizarse como:

Donde es el potencial de fuerza en el punto considerado en la aerodinámica. Por ejemplo, para la gravedad de la Tierra = gz.
Multiplicando con la densidad del fluido ρ, la ecuación (A) puede ser reescrita como:

o:
![]()
donde
- q = 1/2ρv2 es presión dinámica,
- h = z + p/ρg es la cabeza piezométrica o cabeza hidráulica (la suma de la elevación z y la cabeza de presión) y
- p0 = p + q es la presión total (la suma de la presión estática p y la presión dinámica q).
La constante en la ecuación de Bernoulli puede ser normalizada. Un enfoque común es en términos de cabeza total o cabeza de energía H:
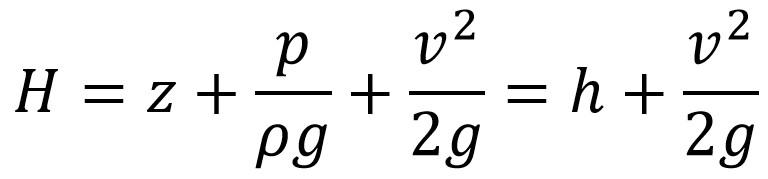
Las ecuaciones anteriores sugieren que hay una velocidad de flujo en la cual la presión es cero, y a velocidades aún más altas la presión es negativa. La mayoría de las veces, los gases y líquidos no son capaces de presión absoluta negativa, o incluso presión cero, por lo que claramente la ecuación de Bernoulli deja de ser válida antes de que se alcance la presión cero. En líquidos – cuando la presión es demasiado baja – se produce cavitación. Las ecuaciones anteriores utilizan una relación lineal entre la velocidad de flujo al cuadrado y la presión. A velocidades de flujo más altas en gases, o para ondas sonoras en líquidos, los cambios en la densidad de masa se vuelven significativos, de modo que la suposición de densidad constante es inválida.
Ejemplo 1: Por un canal irregular al nivel del suelo fluye agua con una presión inicial de 25 Pa. Si el volumen del agua en el inicio del canal es de 7l a una velocidad de 12 m/s, ¿Cual es la velocidad final, si la presión aumenta a 26 Pa?
Tenemos que, como la ecuación de Bernoulli da como resultado una constante, entonces se cumple que:

Ya que el canal está a nivel del suelo, la altura inicial se mantiene hasta el final. La ecuación se simplifica de la siguiente manera:
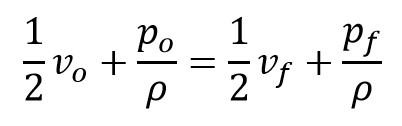
Despejando la velocidad final, quedaría:

Implementando este despeje en Python, sería:
def velFinal(vi,pi,pf,d) -> float: # Función que calcula la velocidad final utilizando
return vi + 2*(pi-pf)/d # la ecuación de Bernoulli
vi = 12 # Velocidad inicial del fluido
pi = 25 # Presion inicial del fluido
pf = 26 # Presion final del fluido
d = 0.997 # Densidad del agua
print("La velocidad final del agua será: " + str(volFinal(vi,pi,pf,d)))
Ejemplo 2: Con el resultado del ejercicio 1, calcule la densidad del fluido en el caso de que no se especificara que el fluido es agua.
Partiendo nuevamente de la ecuación de Bernoulli, se hace el despeje de la densidad del fluido:

Luego, el programa para resolver el problema sería:
def densidad(pi,pf,vi,vf) -> float: # Función que calcula la densidad de un fluido
return 2*(pi-pf)/(vf-vi) # utilizando la ecuación de Bernoulli
vi = 12 # Velocidad inicial del fluido
vf = 10 # Velocidad final del fluido
pi = 25 # Presión inicial del fluido
pf = 26 # Presión final del fluido
print("La densidad del fluido es: " + str(densidad(pi,pf,vi,vf)))
Ejemplo 3: Partiendo de los resultados anteriores, calcule la presión inicial del fluido en caso de que fuera desconocida.
Partiendo de la ecuación de Bernoulli, se despeja la presión inicial de la siguiente forma:
La solución al problema en Python sería:
def presion(d,vf,vi,pf) -> float: # Función que calcula la presión inicial de un
return (d*(vf-vi)/2)+pf # sistema utilizando la ecuación de Bernoulli
vi = 12 # Velocidad inicial del fluido
vf = 10 # Velocidad final del fluido
pf = 26 # Presión final del fluido
d = 0.997 # Densidad del agua
print("La presión inicial del sistema es: " + str(presion(d,vf,vi,pf)))
Forma simplificada
En muchas aplicaciones de la ecuación de Bernoulli, el cambio en el término ρgz a lo largo de la línea aerodinámica es tan pequeño comparado con los otros términos que puede ser ignorado. Por ejemplo, en el caso de una aeronave en vuelo, el cambio de altura z a lo largo de una línea aerodinámica es tan pequeño que el término ρgz puede omitirse. Esto permite que la ecuación anterior se presente de la siguiente forma simplificada:
donde p0 se llama “presión total”, y q es “presión dinámica”. Muchos autores se refieren a la presión p como presión estática para distinguirla de la presión total p0 y la presión dinámica q. En Aerodinámica, L. J. Clancy escribe:”Para distinguirlo de las presiones totales y dinámicas, la presión real del fluido, que está asociada no con su movimiento sino con su estado, se refiere a menudo a la presión estática, pero cuando se usa el término presión por sí solo se refiere a esta presión estática”.
La forma simplificada de la ecuación de Bernoulli puede resumirse en la siguiente ecuación de palabras memorable:
presión estática + presión dinámica = presión total
Cada punto en un fluido que fluye constantemente, independientemente de la velocidad del fluido en ese punto, tiene su propia presión estática p y presión dinámica q. Su suma p + q se define como la presión total p0. La importancia del principio de Bernoulli se puede resumir ahora como “la presión total es constante a lo largo de una línea aerodinámica”.
Si el flujo de fluido es irrotacional, la presión total en cada aerodinámica es la misma y el principio de Bernoulli se puede resumir como “la presión total es constante en todas partes en el flujo de fluido”. Es razonable suponer que el flujo irrotacional existe en cualquier situación en la que un gran cuerpo de fluido fluye más allá de un cuerpo sólido. Ejemplos de ello son las aeronaves en vuelo y los buques que se mueven en aguas abiertas. Sin embargo, es importante recordar que el principio de Bernoulli no se aplica en la capa límite o en el flujo de fluido a través de tubos largos.
Si el flujo de fluido en algún punto a lo largo de una línea aerodinámica es llevado a reposo, este punto se llama punto de estancamiento, y en este punto la presión total es igual a la presión de estancamiento.
Aplicabilidad de la ecuación de caudal incompresible al flujo de gases
La ecuación de Bernoulli es a veces válida para el flujo de gases: siempre que no haya transferencia de energía cinética o potencial desde el flujo de gas a la compresión o expansión del gas. Si tanto la presión del gas como el volumen cambian simultáneamente, entonces se trabajará en o por el gas. En este caso, la ecuación de Bernoulli -en su forma de flujo incompresible- no puede ser asumida como válida. Sin embargo, si el proceso de gas es enteramente isobárico, o isocórico, entonces no se hace ningún trabajo en o por el gas, (por lo que el simple balance de energía no se altera). Según la ley del gas, un proceso isobárico o isocórico es normalmente la única manera de asegurar una densidad constante en un gas. También la densidad del gas será proporcional a la relación de presión y temperatura absoluta, sin embargo, esta relación variará con la compresión o expansión, sin importar qué cantidad de calor no cero se agregue o se elimine. La única excepción es si la transferencia neta de calor es cero, como en un ciclo termodinámico completo, o en un proceso individual isentrópico (sin fricción adiabático), e incluso entonces este proceso reversible debe ser invertido, para restaurar el gas a la presión original y al volumen específico, y por lo tanto a la densidad. Sólo entonces es aplicable la ecuación original, no modificada de Bernoulli. En este caso, la ecuación se puede utilizar si la velocidad de flujo del gas es lo suficientemente inferior a la velocidad del sonido, de manera que se puede ignorar la variación en la densidad del gas (debido a este efecto) a lo largo de cada línea de flujo. El flujo adiabático a menos de Mach 0.3 se considera generalmente bastante lento.
Flujo de potencial inestable
La ecuación de Bernoulli para el flujo potencial inestable se utiliza en la teoría de las ondas superficiales oceánicas y la acústica.
Para un flujo irrotacional, la velocidad de flujo se puede describir como gradiente ∇φ de un potencial de velocidad φ. En ese caso, y para una densidad constante ρ, las ecuaciones de momento de las ecuaciones de Euler pueden ser integradas a:

Que es una ecuación de Bernoulli válida también para flujos que dependen de la inestabilidad o del tiempo. Aquí ∂φ/∂t denota el derivado parcial del potencial de velocidad φ con respecto al tiempo t, y v = |∇φ| es la velocidad de flujo. La función f(t) depende sólo del tiempo y no de la posición en el fluido. Como resultado, la ecuación de Bernoulli en algún momento t no sólo se aplica a lo largo de una cierta línea aerodinámica, sino en todo el dominio de los fluidos. Esto también es cierto para el caso especial de un flujo continuo irrotacional, en cuyo caso f es una constante.
Se puede hacer f(t) igual a cero incorporándolo en el potencial de velocidad utilizando la transformación.

dando lugar a:

Tenga en cuenta que la relación entre el potencial y la velocidad del flujo no se ve afectada por esta transformación:∇Φ = ∇φ.
La ecuación de Bernoulli para el flujo potencial inestable también parece jugar un papel central en el principio varicional de Lucas, una descripción variada de los flujos de superficie libre usando el principio Lagrangiano (no confundir con las coordenadas Lagrangianas).
Ecuación de caudal compresible
Bernoulli desarrolló su principio a partir de sus observaciones sobre los líquidos, y su ecuación es aplicable sólo a fluidos incompresibles, y fluidos compresibles hasta el número Mach aproximadamente 0.3. Es posible utilizar los principios fundamentales de la física para desarrollar ecuaciones similares aplicables a los fluidos compresibles. Existen numerosas ecuaciones, cada una adaptada para una aplicación particular, pero todas son análogas a la ecuación de Bernoulli y todas se basan en nada más que en los principios fundamentales de la física, como las leyes del movimiento de Newton o la primera ley de la termodinámica.
Flujo comprimido en la dinámica de fluidos
Para un fluido compresible, con una ecuación de estado barotrópica, y bajo la acción de fuerzas conservadoras,

donde:
- p es la presión
- ρ es la densidad y ρ(p’) indica que es una función de presión
- v es la velocidad de flujo
- Ψ es el potencial asociado al campo de fuerza conservador, a menudo el potencial gravitacional.
En situaciones de ingeniería, las elevaciones son generalmente pequeñas comparadas con el tamaño de la Tierra, y las escalas de tiempo del flujo de fluidos son lo suficientemente pequeñas para considerar la ecuación de estado como adiabática. En este caso, la ecuación anterior para un gas ideal se convierte:

donde, además de los términos enumerados anteriormente:
- γ es la proporción de los calores específicos del fluido
- g es la aceleración debida a la gravedad
- z es la elevación del punto por encima de un plano de referencia
En muchas aplicaciones de flujo compresible, los cambios de elevación son insignificantes en comparación con otros términos, por lo que el término gz puede omitirse. Una forma muy útil de la ecuación es entonces:
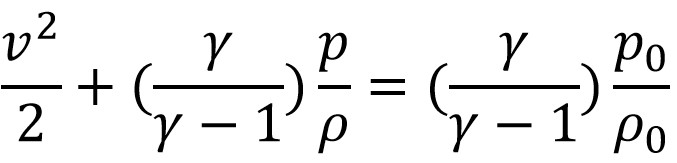
donde:
- p0 es la presión total
- ρ0 es la densidad total
Flujo compresivo en termodinámica
La forma más general de la ecuación, adecuada para su uso en termodinámica en caso de (quasi) flujo constante, es:

Aquí w es la entalpía por unidad de masa, que también se escribe a menudo como h (no confundir con “cabeza” o “altura”).
Tenga en cuenta que w = ε + p/ρ donde ε es la energía termodinámica por unidad de masa, también conocida como energía interna específica. Por lo tanto, para una energía interna constante ε la ecuación se reduce a la forma de flujo incompresible.
La constante en el lado derecho es a menudo llamada la constante de Bernoulli y denotada b. Para un flujo adiabático constante e invisible sin fuentes adicionales o sumideros de energía, b es constante a lo largo de cualquier línea de corriente dada. De manera más general, cuando b puede variar a lo largo de las líneas aerodinámicas, sigue siendo un parámetro útil, relacionado con la “cabeza” del fluido (ver más abajo).
Cuando el cambio en Ψ puede ser ignorado, una forma muy útil de esta ecuación es:

Donde w0 es entalpía total. Para un gas perfecto desde el punto de vista calórico, como un gas ideal, la entalpía es directamente proporcional a la temperatura, lo que conduce al concepto de la temperatura total (o estancamiento).
Cuando las ondas de choque están presentes, en un marco de referencia en el que el choque está estacionario y el flujo es estable, muchos de los parámetros de la ecuación de Bernoulli sufren cambios bruscos al pasar a través del choque. Sin embargo, el propio parámetro Bernoulli no se ve afectado. Una excepción a esta regla son los choques radiativos, que violan los supuestos que conducen a la ecuación de Bernoulli, a saber, la falta de sumideros o fuentes de energía adicionales.
Aplicaciones
En la vida cotidiana moderna hay muchas observaciones que se pueden explicar con éxito mediante la aplicación del principio de Bernoulli, a pesar de que ningún fluido real es completamente invisible y una pequeña viscosidad a menudo tiene un gran efecto en el flujo.
- El principio de Bernoulli se puede utilizar para calcular la fuerza de elevación en un perfil aéreo, si se conoce el comportamiento del flujo de fluido en las inmediaciones de la lámina. Por ejemplo, si el aire que pasa por la superficie superior de una aeronave se mueve más rápido que el aire que pasa por la superficie inferior, el principio de Bernoulli implica que la presión sobre las superficies de la aeronave será más baja por encima que por debajo. Esta diferencia de presión produce una fuerza de elevación ascendente. Siempre que se conozca la distribución de la velocidad por las superficies superior e inferior de un ala, las fuerzas de elevación pueden calcularse (en una buena aproximación) utilizando las ecuaciones de Bernoulli -establecidas por Bernoulli más de un siglo antes de que se utilizaran las primeras alas artificiales para el vuelo. El principio de Bernoulli no explica por qué el aire fluye más rápido por encima de la parte superior del ala y más lento por debajo. Vea el artículo sobre la elevación aerodinámica para más información.
- El carburador utilizado en muchos motores alternativos contiene un venturi para crear una región de baja presión que aspira combustible al carburador y lo mezcla completamente con el aire entrante. La baja presión en la garganta de un venturi puede explicarse por el principio de Bernoulli; en la garganta estrecha, el aire se mueve a su velocidad más rápida y, por lo tanto, a su presión más baja.
- Un inyector en una locomotora de vapor (o caldera estática).
- El tubo pitot y el puerto estático de una aeronave se utilizan para determinar la velocidad del aire de la aeronave. Estos dos dispositivos están conectados al indicador de velocidad del aire, que determina la presión dinámica del flujo de aire que pasa por el avión. La presión dinámica es la diferencia entre la presión de estancamiento y la presión estática. El principio de Bernoulli se utiliza para calibrar el indicador de velocidad aerodinámica de modo que muestre la velocidad aerodinámica indicada apropiada para la presión dinámica.
- La velocidad de flujo de un fluido se puede medir utilizando un dispositivo como un medidor Venturi o una placa de orificio, que se puede colocar en una tubería para reducir el diámetro del flujo. Para un dispositivo horizontal, la ecuación de continuidad muestra que para un fluido incompresible, la reducción en el diámetro causará un aumento en la velocidad de flujo del fluido. A continuación, el principio de Bernoulli demuestra que debe haber una disminución de la presión en la región de diámetro reducido. Este fenómeno se conoce como efecto Venturi.
- La tasa de drenaje máxima posible para un tanque con un orificio o grifo en la base puede calcularse directamente a partir de la ecuación de Bernoulli, y es proporcional a la raíz cuadrada de la altura del fluido en el tanque. Esta es la ley de Torricelli, lo que demuestra que la ley de Torricelli es compatible con el principio de Bernoulli. La viscosidad disminuye esta tasa de drenaje. Esto se refleja en el coeficiente de descarga, que es una función del número de Reynolds y la forma del orificio.
- El agarre Bernoulli se basa en este principio para crear una fuerza adhesiva sin contacto entre la superficie y la pinza.


