Curso intensivo en Redes Neuronales Multicapa o Perceptrones Multicapa

Las Redes Neurales Artificiales son un área de estudio fascinante, aunque pueden ser intimidantes cuando acabamos de empezar. Hay una gran cantidad de terminología especializada que se utiliza al describir las estructuras de datos y algoritmos utilizados en este campo.

Descripción general del curso de Deep Learning con Multicapa Perceptrones

Vamos a cubrir mucho terreno en esta lección. He aquí una idea de lo que nos espera:

1.  Perceptrones multicapa.
2.  Neuronas, Pesos y Activaciones.
3. Redes de Neuronas.
4. Redes de formación.

Perceptrones multicapa o Redes Neuronales

El campo de las redes neurales artificiales es a menudo sólo llamado Redes Neuronales o Perceptrones Multicapa. Un Perceptrón es una sola neurona que fue el precursor de las redes neuronales más grandes. Es un viejo estudio que investiga como modelos simples de cerebros biológicos pueden ser usados para resolver tareas computacionales dificiles como las tareas de modelado predictivo que vemos en el aprendizaje automático. El objetivo no es crear un sistema del cerebro, sino desarrollar algoritmos y estructuras de datos robustos que nos permitan modelar problemas de difíciles.
El poder de las redes neuronales proviene de su capacidad para aprender la representación en sus datos de entrenamiento y cómo relacionarlos mejor con la variable de salida que desea predecir. En este sentido las redes neuronales aprenden un mapeo. Matemáticamente, son capaces de aprender cualquier función de mapeo y han demostrado ser un algoritmo de aproximación universal. La capacidad predictiva de las redes neuronales proviene de la estructura jerárquica o multicapa de las redes. La estructura de datos puede seleccionar (aprender a representar) características a escalas diferentes o resoluciones y combinarlas en características de orden superior. Por ejemplo podemos ir de líneas, a colecciones de líneas para representar formas.

Neuronas

El bloque de construcción de las redes neuronales son las neuronas artificiales. Éstas son sencillas unidades computacionales que han ponderado las señales de entrada y producen una señal de salida utilizando una función de activación.

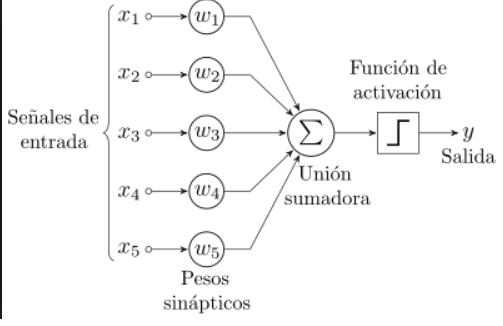
Pesos Neuronales o sinápticos

Es posible que esté familiarizado con la regresión lineal, en cuyo caso los pesos de las entradas son muy altos como los coeficientes usados en una ecuación de regresión. Como la regresión lineal, cada neurona también tiene un sesgo que puede ser considerado como una entrada que siempre tiene el valor 1.0 y también debe ser ponderado. Por ejemplo, una neurona puede tener dos entradas, en cuyo caso requiere tres pesos. Uno para cada entrada y otro para el sesgo.
Los pesos se inicializan a menudo a valores aleatorios pequeños, tales como valores en el rango de 0 a 0,3, aunque se pueden utilizar esquemas de inicialización más complejos. Como la regresión lineal, los pesos más grandes indican una mayor complejidad y fragilidad del modelo.

Activación o función de activación

Las entradas ponderadas se suman y pasan a través de una función de activación, a veces llamada a función de transferencia. Una función de activación es una asignación simple de la entrada ponderada sumada a la de la neurona. Se denomina función de activación porque gobierna el umbral en que la neurona es activada y la fuerza de la señal de salida. Un paso históricamente sencillo es que se utilizaban funciones de activación cuando la suma de las entradas estaban por encima de un umbral, por ejemplo 0.5, entonces la neurona daría un valor de 1.0, de lo contrario daría un valor de 0.0.
Tradicionalmente se utilizan funciones de activación no lineales. Esto permite a la red combinar las entradas de maneras más complejas y a su vez proporcionar una capacidad más rica en las funciones que pueden modelar. Se utilizaron funciones no lineales como la función logística, también llamada función sigmoide, que emite un valor entre 0 y 1 con una distribución en forma de s, y la función tangente hiperbólica, también llamada Tanh, que emite la misma distribución en el rango de -1 a +1. Más recientemente, se ha demostrado que la función de activación rectificadora proporciona mejores resultados.

Redes de Neuronas

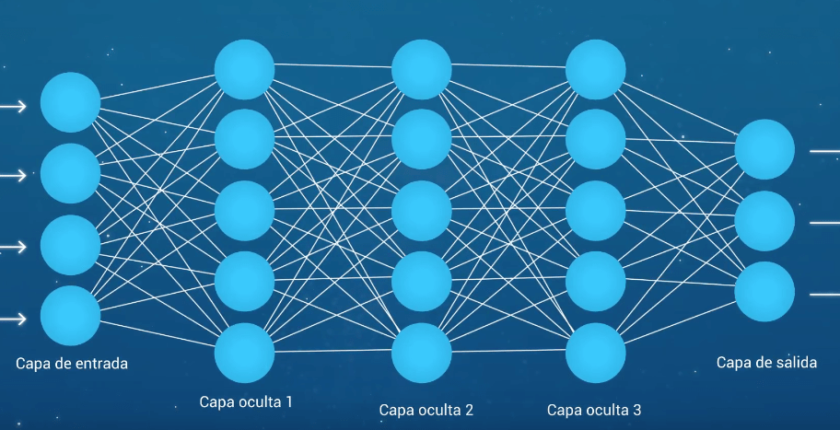
Las neuronas están dispuestas en redes de neuronas. Una fila de neuronas se llama una capa y una  red puede tener múltiples capas. La arquitectura de las neuronas en la red se llama a menudo la topología de la red.

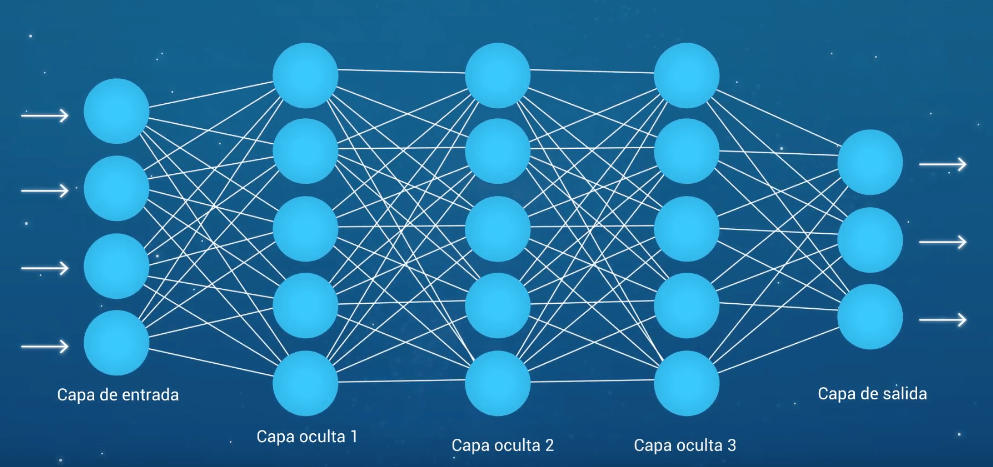
Entrada o capas visibles

La capa inferior o a la izquierda de la imagen de arriba que toma entrada de su dataset (conjunto de datos) se llama la capa visible, porque es la parte expuesta de la red. A menudo, una red neuronal se dibuja con una capa visible con una por valor de entrada o columna en su conjunto de datos. Estas no son neuronas como se describió anteriormente, sino que simplemente pasa el valor de entrada a la siguiente capa.

Capas ocultas

Las capas después de la capa de entrada se llaman capas ocultas porque no están expuestas directamente a la entrada. La estructura de red más simple es tener una sola neurona en la capa oculta que directamente emite el valor. Dados los incrementos en la potencia de computación y en las eficientes librerías se pueden construir redes neuronales muy profundas . El Deep Learning se refiere a tener muchas capas ocultas en tu red neural. Son profundas porque habrían sido inimaginablemente lentas para entrenar históricamente, pero puede tomar segundos o minutos entrenar usando técnicas y hardware modernos.

Capa de salida

La última capa oculta se llama capa de salida y es responsable de emitir un valor o vector de valores que corresponden al formato requerido para el problema. La elección de la función de activación en la capa de salida está fuertemente limitada por el tipo de problema que usted están modelando. Por ejemplo:

• Un problema de regresión puede tener una neurona de salida única y la neurona puede no tener función de activación.
• Un problema de clasificación binaria puede tener una neurona de salida única y utilizar un sigmoi de función de activación para emitir un valor entre 0 y 1 que represente la probabilidad de predecir un valor para la clase primaria. Esto se puede convertir en un valor de clase nítido usando un umbral de 0.5 y ajustar valores menores que el umbral a 0 de lo contrario a 1.
• Un problema de clasificación multiclase puede tener múltiples neuronas en la capa de salida, una para cada clase. En este caso, se puede utilizar una función de activación softmax para emitir una probabilidad de la red prediciendo cada uno de los valores de clase. Seleccionar la salida con el valor más alto y la probabilidad puede ser utilizada para producir un valor de clasificación de clase nítido.

Redes de capacitación o redes de aprendizaje

Una vez terminada la red neuronal necesita ser entrenada en su conjunto de datos.

Preparación de datos

Usted debe preparar primero sus datos para el entrenamiento en una red neuronal. Los datos deben ser numéricos, como por ejemplo valores reales. Si tiene datos categóricos, como un atributo de sexo con los valores macho y hembra, puede convertirlo a una representación de valor real llamada codificación en caliente. Este es donde se añade una nueva columna para cada valor de clase (dos columnas en el caso del sexo de los hombres y las mujeres) y se añade un 0 ó 1 para cada fila dependiendo del valor de la clase para esa fila.

Esta misma codificación en caliente se puede utilizar en la variable de salida en problemas de clasificación con más de una clase. Esto crearía un vector binario a partir de una sola columna que es fácil de comparar directamente con la salida de la neurona en la capa de salida de la red, que como hemos descrito anteriormente, produciría un valor para cada clase. Las redes neuronales requieren que la entrada sea de una manera consistente. Puede reescalarlo al rango entre 0 y 1 esto es la normalización. La escala también se aplica a los datos de píxeles de la imagen. Datos tales como palabras pueden ser convertidas en números enteros, tales como el rango de frecuencia de la palabra en el conjunto de datos y otras técnicas de codificación.

Descenso estocástico por gradiente

El clásico y aún preferido algoritmo de entrenamiento para redes neuronales se llama el Descenso de Gradientes Estocástico. Aquí es donde una fila de datos se expone a la red como entrada. La red procesa la entrada hacia delante activando las neuronas hasta que finalmente se produce un valor de salida. Esto se llama un pase adelante en la red. Es el tipo de pase que también es usado después de que la red es entrenada para hacer predicciones sobre nuevos datos. La salida del grafo se compara con la salida esperada y se calcula un error. Este error es entonces propagado a través de la red, en todas las capas y los pesos se actualizan en función del importe que han contribuido al error. Esta inteligente parte de las matemáticas se llama el algoritmo de retropropagación. El proceso se repite para todos los ejemplos en su datos de formación. Una ronda de actualización de la red para todo el conjunto de datos de formación se denomina época o epoch. Una red puede ser entrenada por decenas, cientos o muchos miles de épocas.

Actualizaciones de peso

Los pesos en la red se pueden actualizar a partir de los errores calculados para cada ejemplo de formación y esto se llama aprendizaje en línea. Puede resultar en cambios rápidos pero también caóticos en la red.

Alternativamente, los errores se pueden guardar en todos los ejemplos de formación y la red puede actualizarse al final. Esto se llama aprendizaje por lotes y a menudo es más estable.

Debido a que los conjuntos de datos son tan grandes y debido a las eficiencias computacionales, el tamaño del lote, el número de ejemplos que muestra la red antes de una actualización a menudo se reduce a un número pequeño, como decenas o cientos de ejemplos. El importe que se actualizan las ponderaciones es controlado por un parámetro de congestión llamado velocidad de aprendizaje. También se le llama el tamaño del paso y controla el paso o cambio hecho a los pesos de red para un error dado. A menudo el aprendizaje es pequeño como 0.1 o 0.01 o menor. La ecuación de actualización se puede complementar con términos de congestión adicionales que usted puede establecer.

• Momentum es un término que incorpora las propiedades de la anterior actualización de peso para permitir que los pesos continúen cambiando en la misma dirección incluso cuando hay menos error que se está calculando.
• La Decadencia de la Tasa de Aprendizaje se utiliza para disminuir la tasa de aprendizaje en epochs para permitir realizar grandes cambios en los pesos al principio y pequeñas modificaciones en la sintonía de cambios posteriores en el programa de entrenamiento.

Predicción

Una vez que una red neuronal ha sido entrenada, puede ser usada para hacer predicciones. Puede hacer predicciones sobre datos de prueba o validación para estimar la habilidad del modelo sobre datos no vistos. También puede desplegarlo operativamente y usarlo para hacer predicciones continuamente. La topología de red y el conjunto final de pesos es todo lo que necesita para guardar el modelo. Las predicciones se realizan proporcionando la entrada a la red y realizando un paso adelante que le permite generar un resultado que se puede utilizar como predicción.

Resumen de Curso en Multicapa Perceptrones

En esta lección usted descubrió las redes neuronales artificiales para machine learning. Aprendiste:

• Cómo las redes neuronales no son modelos del cerebro sino modelos computacionales para resolver problemas complejos de machine learning.
• Que las redes neuronales están compuestas de neuronas que tienen pesos y funciones de activación.
• Las redes están organizadas en capas de neuronas y son entrenadas usando el algoritmo de gradiente estocástico de descenso.
• Que es una buena idea preparar sus datos antes de entrenar un modelo de red neuronal.

Siguiente

➡ Ahora conoces los fundamentos de los modelos de redes neuronales.
Si quieres saber mas te recomendamos realizar este curso:

Curso de Deep Learning